Time dilation calculator

This page contains a time dilation calculator. To calculate the time dilation enter a percentage of the speed of light (c) and press the button to continue. A distance/time dilation calculator is available further down the page.

Legal Notice: This website does not accept liability for anyone arriving a few seconds late after a journey of millions of light years as a result of using these calculators. We advise packing an extra sandwich, just in case.

Here are some examples to try:

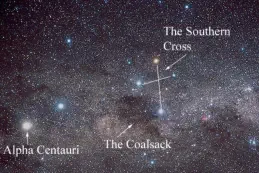
Apart from the Sun the nearest stars to us form the Alpha Centauri system. It consists of three stars: Alpha Centauri A, Alpha Centauri B and the small, faint red dwarf star Alpha Centauri C, otherwise known as Proxima Centauri. The system is found near The Southern Cross constellation, as shown on the right. The distance from Earth to the Alpha Centauri group is 4.37 light years, or 41,343,000,000,000 kilometres (25,690,000,000,000 miles). Even our nearest neighbour is very far away…

Betelgeuse is a well-known and spectacular star found in the constellation Orion. It’s classed as a red supergiant and is one of the largest stars seen with the naked eye. It’s not only 100,000 times brighter than the Sun, but about 1000 times its diameter. The distance from Earth to the Betelgeuse is about 640 light years.

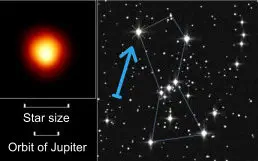
The centre of the Milky Way: Our galaxy, the Milky Way, is about 100,000 light years across. The Sun lies on the Sagittarius arm and is about 26,000 light years from the centre, which very likely contains a supermassive black hole, called Sagittarius A*, occasionally sucking in and crushing whole stars, further adding to its mass. The pictures show the black hole and its location (circled) at the heart of the Milky Way.

The Andromeda Galaxy: The nearest major galaxy to our own is the Andromeda Galaxy, also known as M31. It’s over twice the diameter of the Milky Way at about 220,000 light years. Although our nearest major galactic neighbour, it’s still around 2,500,000 light years away. It’s also the furthest object that most people can see with the naked eye. On a clear night at the right time of year it can be seen as a faint chalk-like smudge in the constellation Andromeda.

The furthest known galaxy (as of 2024) goes by the name of GN-z11. It’s around 13.4 billion light years away (13,400,000,000 light years). An interesting point to note is that while the light we see it by started off on its journey over 13 billion years ago that’s as measured by our Earth-bound clocks. Because it’s light in a vacuum it has a 100% dilation factor and so, from the perspective of the light itself, it got here instantly and travelled zero distance in doing so. As the English astronomer Sir Arthur Eddington said: Not only is the universe stranger than we imagine, it is stranger than we can imagine. Even travelling at 99.9999999% of the speed of light it would still take over half a million years to get there.

Perhaps one of the strangest aspects of special relativity is that distances shrink in the direction of motion. This may not seem so important at first but it leads to something quite remarkable. Common sense tells us that if a spaceship travels at 90% of the speed of light then it would take about 11 years to reach a star 10 light years away, and that is indeed what a stationary observer would see and measure. However, for the spaceship not only time but distance will dilate and the star would be reached in only about 4.8 years. Going even faster reduces the time taken by an ever increasing amount. To see how long it would take to reach a star or galaxy when travelling at different speeds enter a percentage of the speed of light (c) and a distance in light years to the star or galaxy in the boxes below and click Calculate. You may also want to try the examples listed below the calculation box:

Time Dilation Calculator

NEW! Quick and Easy SuperFast Guides NEW!

[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ] [ Black Holes ] [ Twin Paradox ] [ Time Dilation Formula ]