



Advertisement

The Central Problem of Relativity
The Italian scientist and mathematician Galileo Galilei (1564 - 1642) is perhaps most famous for his use of early
telescopes in order to make astronomical observations. He is considered one of the founders of modern science and in
many ways was far ahead of his time. He made many contributions to science, such as the mechanics of falling bodies
and moving projectiles. In doing so he also formulated the first modern theory of relativity. As with much of Newton's work,
Galileo's theory turned out to be correct only at "low" speeds but it's still instructive and helps in the understanding of
Einstein's Special Theory of Relativity.
Galileo Galilei (1564 – 1642)
If an event takes place and two people see it from different locations how can they agree on when and were it
happened? This question, in one form other, is called the "central problem of relativity". At first glance this problem has
quite an easy solution. Let's imagine you and I both see a stationary firework explode. You are standing in one location
and I am standing a little further away. As we see the explosion we both look at our (synchronised) watches and note the
time. We then pace out the distance to the remnants of the firework. We should agree on the time of the explosion but
our distance measurements will be different. In other words we will have both witnessed the same event relative to each
other.
So far so good. Now let's try another experiment. This time instead of both watching a stationary event we will add some
movement. You are on an aircraft travelling at 500 mph and I am on the ground. You decide to go and speak to the pilot
and walk forward in the aeroplane towards him or her at 5 mph. What is your speed now? I see you move at 505 mph,
but you feel that you are moving at only 5 mph. Again, we have to take our relative positions into account but this time
we need to include the movement involved.
This is all so easy that we don't even have to think about it in everyday life. Instead of being as difficult as is sometimes
supposed, relativity is actually a very old and very simple idea. There is really only one problem; what co-ordinate
system should we use? 400 years ago Galileo thought he knew...


Stationary Frames
x’ = x - Vt
y’ = y
z’ = z
t’ = t
In order to work out when and where an event took place we need to take the viewpoints of different observers into
account. One way to do this, and which is adequate at speeds much lower than the speed of light, is to use the Galilean
transformation co-ordinate equations. Stated mathematically they are:
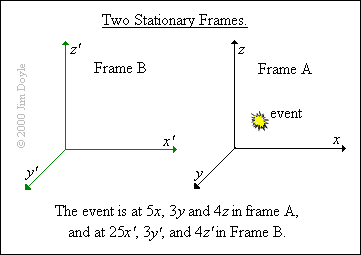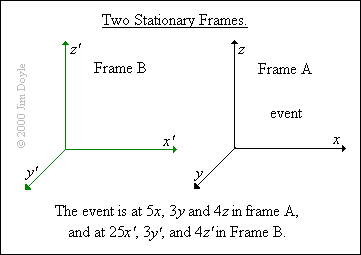
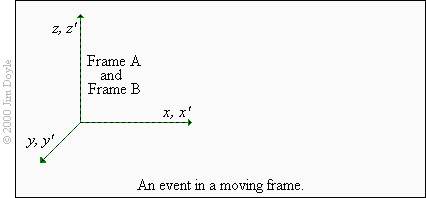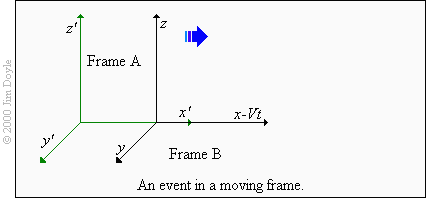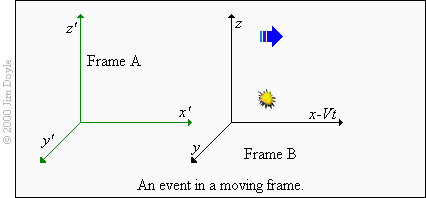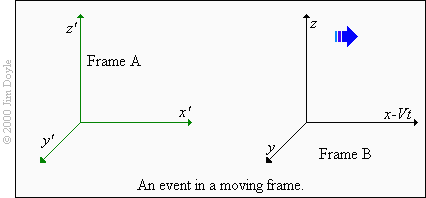
To understand what this means consider two 'frames', A and B, in space. An event takes place in frame A and we want
to be able to say where and when that event took place. This is quite easy; we can give the event the spatial co-
ordinates x, y, and z, and a time co-ordinate of of t. So, for example, we could say that the event took place at 5x, 3y and
4z, and at a time of 6t.
Now let's imagine that we observed the same event from another place in space, from frame B. What would the co-
ordinates of the same event be now? If both frame A and frame B are stationary with respect to each other this is also
simple. We just need to apply an extra measurement factor to each of the co-ordinates in frame A. Once we have done
this we can call the co-ordinates x, y, z and t in frame A and x’, y’, z’ and t’ in frame B.
For example, in frame A the x-co-ordinate of the event was 5x but as measured from frame B it might be 25x. In other
words, we would have to multiply any x event in frame A by 5 to find out the co-ordinates of the same event (x') in the
origin of frame B:
Now let's add movement, and therefore time, into the picture.
Moving Frames
Imagine that a train passes you and after 6 seconds you see a flash of light from the train. The train is moving at 80 mph.
How far away was the train when the light flashed? To make our calculations easier we will convert miles per hour into
metres per second: 80 mph is about 130 km/h, which is about 36 metres per second
We need to use the x-co-ordinate transformation to work this out, but there is something we might like to do first. We have
chosen our origin (x' and x) to be at zero (that is, the place we were standing at when the train went by). If we use x' = x -
Vt as it is we will get a negative result. In reality this isn't a problem, but it looks a little odd. So, for the sake of clarity, we
will change the equation to be x' = x + Vt. Now, let's plug the numbers into the equation and find the answer:
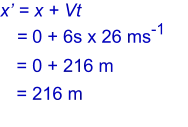
So, as viewed from the stationary frame the flash of light was about 216 metres away. In other words the x'-co-ordinate is
216 m. As viewed from the train the event was zero metres away. That is, the x-co-ordinate is 0 m.
The example given is really very simple but it illustrates an important point; we have sets of co-ordinates that are relative
to each other. We have a simple "theory of relativity", and one that works very well in most cases. The only problem is,
ultimately, it's wrong.
Common Sense versus Reality
Galileo's relativity can be thought of as nothing more than common sense with a few numbers added to it. Indeed, it
works very well at "low" speeds and is still in use today. Even the co-ordinate systems used to track and guide the fastest
rockets use a version of his equations. So what's wrong with it?
We have seen from other pages in this series that “moving clocks run slow.” The faster the clock moves as a percentage
of the speed of light the more it slows down. What's more, this has been demonstrated to be correct in all sorts of
experiments and even practical applications such as the GPS system. In Galileo's system time is constant and clocks
simply can't change their rate. If we use x’ = x - Vt then the observed time will always be the same in both the moving and
stationary frames. For this reason alone we have to reject Galilean co-ordinate transformations in the wider sense.
Another problem stems from the spatial co-ordinates. The space-time dilation equations as applied by Einstein tell us that
distances shrink in the direction of motion. According to Galileo's system this is not the case. His equations state that an
object will always remain the same length regardless of its speed.
For example, imagine a rod accelerating to a very high speed, say 90% of the speed of light (0.9 c). We can label the
ends of the rod (L
1
and L
2
) and then apply the x-co-ordinate transformation equation to measure its length. The diagram
below shows what Galileo's system predicts:
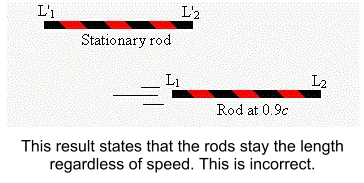
From experimental evidence as well as modern theoretical predictions we know that the moving rod would shrink in the
direction of motion and so we have another failure of the Galilean transformation equations.
Although Galilean relativity matches our own common sense and is certainly a good approximation at speeds much lower
than that of light it is ultimately wrong. For a system of co-ordinate transformation equations to be correct under all
circumstances we have to take space and time dilation into account. This is accomplished using Einstein's Special Theory
of Relativity.

Postscript on Galileo
This page may have given the impression that Galileo and his ideas can be dismissed. That is far from being the case.
He was one of the first people to start to quantify the universe around us and as such was one of a small handful of
people that turned speculative and fuzzy ideas into modern science. In doing so he made many lasting contributions to
physics. To list just a few:
The discovery of the four largest moons orbiting Jupiter. This was the first evidence that at least some
bodies in the universe do not orbit the Earth.
The relationship between a swinging pendulum's length and the time taken for it to return to its starting
position. This discovery allowed the first accurate mechanical clocks to be constructed.
The realisation that when two objects of different masses are dropped at the same time they both reach
the ground at the same time (providing there is not dissimilar air resistance on the objects). Newton used
this information in forming his Theory of Universal Gravitation.



It is also astonishing that he built time into some of his equations long before accurate clocks were available.
In his lifetime Galileo was often dismissed by fellow academics and punished by the church for holding heretical ideas,
particularly that the Earth revolved around the Sun. He was sentenced to permanent house arrest by the Inquisition in
1633 and died, still under house arrest, nine years later. In 1979 the Catholic Church started an investigation into
Galileo's condemnation and in 1992 a papal commission acknowledged that an error had been made.
In 1989 NASA launched the Galileo space probe. Its mission was to provide information about Jupiter and its four largest
moons, a task it carried out with enormous success, making many important discoveries, before being plunged into the
Jovian atmosphere in 2003.

An artist’s impression of the Galileo space probe passing Jupiter’s moon Io

Galileo Galilie
E = mc2 Galileo
Advertisement



Advertisement





The Italian scientist and mathematician Galileo Galilei (1564-
1642) is perhaps most famous for his use of early telescopes in
order to make astronomical observations. He is considered one
of the founders of modern science and in many ways was far
ahead of his time. He made many contributions to science, such
as the mechanics of falling bodies and moving projectiles. In
doing so he also formulated the first modern theory of relativity.
As with much of Newton's work, Galileo's theory turned out to be
correct only at "low" speeds but it's still instructive and helps in
the understanding of Einstein's Special Theory of Relativity.

Galileo Galilei (1564 – 1642)
The Central Problem of Relativity
If an event takes place and two people see it from different
locations how can they agree on when and were it happened?
This question, in one form other, is called the "central problem of
relativity". At first glance this problem has quite an easy solution.
Let's imagine you and I both see a stationary firework explode.
You are standing in one location and I am standing a little further
away. As we see the explosion we both look at our
(synchronised) watches and note the time. We then pace out the
distance to the remnants of the firework. We should agree on the
time of the explosion but our distance measurements will be
different. In other words we will have both witnessed the same
event relative to each other.
So far so good. Now let's try another experiment. This time
instead of both watching a stationary event we will add some
movement. You are on an aircraft travelling at 500 mph and I am
on the ground. You decide to go and speak to the pilot and walk
forward in the aeroplane towards him or her at 5 mph. What is
your speed now? I see you move at 505 mph, but you feel that
you are moving at only 5 mph. Again, we have to take our
relative positions into account but this time we need to include
the movement involved.
This is all so easy that we don't even have to think about it in
everyday life. Instead of being as difficult as is sometimes
supposed, relativity is actually a very old and very simple idea.
There is really only one problem; what co-ordinate system should
we use? 400 years ago Galileo thought he knew...


Stationary Frames
In order to work out when and where an event took place we
need to take the viewpoints of different observers into account.
One way to do this, and which is adequate at speeds much lower
than the speed of light, is to use the Galilean transformation co-
ordinate equations. Stated mathematically they are:
x’ = x - Vt
y’ = y
z’ = z
t’ = t
To understand what this means consider two 'frames', A and B,
in space. An event takes place in frame A and we want to be
able to say where and when that event took place. This is quite
easy; we can give the event the spatial co-ordinates x, y, and z,
and a time co-ordinate of of t. So, for example, we could say that
the event took place at 5x, 3y and 4z, and at a time of 6t.
Now let's imagine that we observed the same event from another
place in space, from frame B. What would the co-ordinates of the
same event be now? If both frame A and frame B are stationary
with respect to each other this is also simple. We just need to
apply an extra measurement factor to each of the co-ordinates in
frame A. Once we have done this we can call the co-ordinates x,
y, z and t in frame A and x’, y’, z’ and t’ in frame B.
For example, in frame A the x-co-ordinate of the event was 5x
but as measured from frame B it might be 25x. In other words,
we would have to multiply any x event in frame A by 5 to find out
the co-ordinates of the same event (x') in the origin of frame B:

Now let's add movement, and therefore time, into the picture.
Moving Frames
Imagine that a train passes you and after 6 seconds you see a
flash of light from the train. The train is moving at 80 mph. How
far away was the train when the light flashed? To make our
calculations easier we will convert miles per hour into metres
per second: 80 mph is about 130 km/h, which is about 36
metres per second
We need to use the x-co-ordinate transformation to work this
out, but there is something we might like to do first. We have
chosen our origin (x' and x) to be at zero (that is, the place we
were standing at when the train went by). If we use x' = x - Vt as
it is we will get a negative result. In reality this isn't a problem,
but it looks a little odd. So, for the sake of clarity, we will change
the equation to be x' = x + Vt. Now, let's plug the numbers into
the equation and find the answer:
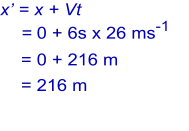
So, as viewed from the stationary frame the flash of light was
about 216 metres away. In other words the x'-co-ordinate is 216
m. As viewed from the train the event was zero metres away.
That is, the x-co-ordinate is 0 m.
The example given is really very simple but it illustrates an
important point; we have sets of co-ordinates that are relative to
each other. We have a simple "theory of relativity", and one that
works very well in most cases. The only problem is, ultimately,
it's wrong.
Galileo's relativity can be thought of as nothing more than
common sense with a few numbers added to it. Indeed, it works
very well at "low" speeds and is still in use today. Even the co-
ordinate systems used to track and guide the fastest rockets use
a version of his equations. So what's wrong with it?
We have seen from other pages in this series that “moving
clocks run slow.” The faster the clock moves as a percentage of
the speed of light the more it slows down. What's more, this has
been demonstrated to be correct in all sorts of experiments and
even practical applications such as the GPS system. In Galileo's
system time is constant and clocks simply can't change their
rate. If we use x’ = x - Vt then the observed time will always be
the same in both the moving and stationary frames. For this
reason alone we have to reject Galilean co-ordinate
transformations in the wider sense.
Another problem stems from the spatial co-ordinates. The space-
time dilation equations as applied by Einstein tell us that
distances shrink in the direction of motion. According to Galileo's
system this is not the case. His equations state that an object will
always remain the same length regardless of its speed.
For example, imagine a rod accelerating to a very high speed,
say 90% of the speed of light (0.9 c). We can label the ends of
the rod (L
1
and L
2
) and then apply the x-co-ordinate
transformation equation to measure its length. The diagram
below shows what Galileo's system predicts:
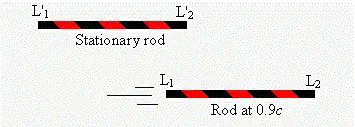
This result states that the rods stay the length
regardless of speed. This is incorrect.
From experimental evidence as well as modern theoretical
predictions we know that the moving rod would shrink in the
direction of motion and so we have another failure of the Galilean
transformation equations.
Although Galilean relativity matches our own common sense and
is certainly a good approximation at speeds much lower than that
of light it is ultimately wrong. For a system of co-ordinate
transformation equations to be correct under all circumstances
we have to take space and time dilation into account. This is
accomplished using Einstein's Special Theory of Relativity.

Postscript on Galileo
This page may have given the impression that Galileo and his
ideas can be dismissed. That is far from being the case. He was
one of the first people to start to quantify the universe around us
and as such was one of a small handful of people that turned
speculative and fuzzy ideas into modern science. In doing so he
made many lasting contributions to physics. To list just a few:
The discovery of the four largest moons orbiting Jupiter.
This was the first evidence that at least some bodies in
the universe do not orbit the Earth.
The relationship between a swinging pendulum's length
and the time taken for it to return to its starting position.
This discovery allowed the first accurate mechanical
clocks to be constructed.
The realisation that when two objects of different masses
are dropped at the same time they both reach the ground
at the same time (providing there is not dissimilar air
resistance on the objects). Newton used this information
in forming his Theory of Universal Gravitation.
It is also astonishing that he built time into some of his
equations long before accurate clocks were available.
In his lifetime Galileo was often dismissed by fellow academics
and punished by the church for holding heretical ideas,
particularly that the Earth revolved around the Sun. He was
sentenced to permanent house arrest by the Inquisition in 1633
and died, still under house arrest, nine years later. In 1979 the
Catholic Church started an investigation into Galileo's
condemnation and in 1992 a papal commission acknowledged
that an error had been made.
In 1989 NASA launched the Galileo space probe. Its mission
was to provide information about Jupiter and its four largest
moons, a task it carried out with enormous success, making
many important discoveries, before being plunged into the
Jovian atmosphere in 2003.

An artist’s impression of the Galileo space probe
passing Jupiter’s moon Io

Common Sense versus Reality
Galileo Galilie
Advertisement


















