
Introduction



Advertisement

The Special Theory of Relativity was proposed in 1905 by Albert Einstein (1879 - 1955). The reason it is "special" is
because it is part of, or a "special case" of, the more comprehensive and complex General Theory of Relativity. The
latter, General Theory, was proposed by Einstein in 1915.

In an everyday co-ordinate system, such as a map, it's possible to specify a location using just dimensional distances.
For example, to someone looking for buried treasure we could say "go east for 20 miles, north for 5 miles, then dig down
30 feet." We have just specified a three dimensional co-ordinate system. To this, Einstein added another factor, that of
time. This still makes sense in our everyday world: "go east for 20 miles, north for 5 miles, dig down 30 feet, and then
wait until 3 o'clock when I will meet you to share the treasure!"
However, if we go at very high speeds, speeds close to the speed of light, things begin to change in a very unexpected
way. The faster we go the more our clock slows down relative to someone standing still; time, for anything moving,
changes. Instead of space and time being separate entities they are the same thing, called space-time. In short:
“moving clocks run slow”.


The theory is based on two principles (postulates):
Physical laws are the same in all frames of reference. That is; any event within a portion of space
(a frame) can be specified by three spatial dimensions (east-west, north-south, up-down) and one
temporal dimension (time). Also, the laws that apply to us in everyday circumstances (such as
Newton's laws) also apply within each frame of reference.
The speed of light is constant. That is, in a vacuum, such as in space, the speed of light is always
the same, regardless of the speed of someone observing it.


The first postulate is seemingly simple and trivial. If I sit and wait an hour in New York, an hour passes. If I sit and wait
an hour in London then an hour also passes. I am, almost exactly, in the same bit of space (frame of reference), moving
around the Sun at the same speed wherever I sit on the Earth. The way time passes in all frames of reference is
governed by the same laws.
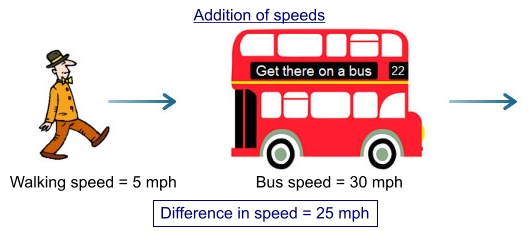
While the first postulate is pretty much what we might expect the second requires a little more explanation. The speed of
light is very close to 300,000 kilometres per second (around 186,300 miles per second). Everyday experience tells us
that if a bus is moving north at 30 miles per hour and we are also walking north at 5 miles per hour then the bus is
moving away from us at 25 miles per hour:
But what if we move in the same direction as a light beam? Let's say we produce a pulse of light into space by quickly
flashing a torch (flashlight) on and off. We then follow the beam of light in a very fast rocket moving at 100,000 km per
second. How fast is the light beam moving away from us? Common sense tells us that it's moving away from us 300,000
km minus 100,000 km per second. In other words, the light beam is 200,000 km per second faster than us. Wrong!
Remember that the speed of light is always the same regardless of our own speed. From our rocket we would see that
the beam of light is still moving away from us at 300,000 km per second! Likewise, if we were moving towards the beam
at a very high speed we would still see the light coming at us at 300,000 km per second! This has enormous, but not
always obvious, implications.
If the speed of light stays the same then something else has to change. That "something" is time.
As odd as it seems time is not constant. More accurately, space-time is not constant. It can be changed, bent and
twisted. The faster we go the more time slows down ("moving clocks run slow"), i.e. time becomes “dilated”. This is only
really noticeable at very high speeds such as those approaching the speed of light; 300,000 km per second (186,300
miles per second), or approximately 7 times around the Earth in a second.
One of the most dramatic consequences of space-time not being constant is that time itself will run at different speeds
as measured by any clock, including own own body clocks. In addition, a stationary clock will measure the passing of
time at a different rate to that of a moving clock, even if both clocks are observed simultaneously. The clocks are each
behaving normally in their respective frames, but different to each other in their relative frames, hence “relativity”.
The twin paradox
Let's have an example. Mary, a 30 year old NASA astronaut, blasts off in her very high speed rocket in the year 2040 on
a 10 year mission to a nearby star. After a short time she is travelling at 270,000 km per second, that is, 90% of the
speed of light. To Mary everything looks normal in her rocket; the clock seems normal and time passes for her the way it
did back on Earth.
Her identical twin sister, Susan, is a NASA ground controller for the mission. Ten years pass on Earth before the rocket
returns and when it does so something is immediately apparent; while the Earth-bound Susan has aged 10 years, her
high-flying "twin" sister has only aged 5 years! How can this be?
Well, again, we are back to "moving clocks run slow". At 90% of the speed of light time slows down to about half of that
relative to someone who is stationary. So while 10 years have passed for Susan only 5 years have passed for Mary
because her "clock" was running at half the speed of those on Earth. This is called the twin paradox. Remember that
while Mary has only aged 5 years she still felt that time was passing normally, i.e. at it’s usual rate. Not only was her
clock running slow as far as any ground based observers are concerned, but her time was running slow.
One question that often crops up is why was it that Susan and her rocket that experienced time dilation and not Mary?
After all, couldn’t we equally regard Susan as standing still and Mary and the Earth as moving away from her?
The answer is that speeds can’t be achieved instantly and it is the acceleration of one body of mass away from another
that determines which body of mass experiences the dilation.
Simple examples of this are found in atomic accelerators. For example, the half-life of a free neutron is about 10
minutes. That is, half of any neutrons will decay (fall apart) in about 10 minutes once unbound from other particles.
However, if accelerated to about 90% of the speed of light then the half-life of the neutrons increases to about 15
minutes, i.e. just as relativity dictates it should (their clocks are running slow). The scientists watching and measuring this
are stationary, relative to the accelerated neutrons, and so they do not experience dilation. In the same way, Susan
accelerated away from Mary and so she is the one who experienced time dilation. (There’s a very good reason why the
machines such as those at CERN are called accelerators.)

Space and Time
Einstein’s Two Postulates
Moving clocks run slow
Time Dilation

The first point tells us that, for example, the distance to any distant star will be reduced the faster we travel towards it
and is covered in more detail on this page. In short, if we travel at about 90% of the speed of light then distances (as
perceived by the traveller) are roughly halved.
The latter two points are connected: Under the "rules" of special relativity the mass of any object appears (to a
stationary observer) to increase as the speed of the object increases. At 90% of the speed of light mass will
approximately double, but at 99% of the speed of light the apparent mass will appear to have increased by about 7
fold. As we get closer to the speed of light the mass increases very dramatically until at the speed of light it would be
infinite. The more mass something has the more energy is required to move it, as we know from everyday experience.
To move something of infinite mass would require infinite energy and this is clearly not possible, hence nothing can
travel faster than light.
We live in a universe dominated by special relativity where faster than light travel isn’t possible. However, there is
some debate amongst physicists as to whether or not a process known as quantum tunnelling allows for certain
particles to travel faster than light under certain conditions. This will require more research in order for the matter to be
resolved one way or another. Even so, such research and debates are outside the scope of special relativity and need
not concern us here.
Is It Real?
This is all well and good, but what evidence is there? After all it's just a "theory". Some clarification is required here.
Unlike its use in the everyday world, scientists use the word theory only when there is substantial and verifiable
evidence for an observed phenomena. In this sense a scientific theory is quite unlike a conjecture or idea, and more
often than not requires a great deal of observational and experimental evidence before attaining the status of theory. In
the case of special relativity there have been very many experiments carried out and all of them have provided
evidence that special relativity is correct. These range from experiments involving sub-atomic particles in high speed
accelerators, as noted earlier, to the slight, but expected, different clock rates of some space exploration vehicles
(such as the Voyager inter-planetary probes) as compared with those on Earth. Even the GPS satellites, which work
by measuring time, have to take relativity into account to stop their clocks quickly becoming unsynchronised with those
on Earth.
One example of supporting evidence for the theory is a much simpler experiment that was first carried out in 1971 and
has been repeated many times since then. Atomic clocks have been carried on aircraft making long flights such as
over the Atlantic ocean. An aircraft, even the fastest, goes at a tiny fraction of the speed of light, but at any speed
"moving clocks run slow". With an atomic clock on the ground and one in the aircraft it's possible to measure the tiny
differences in time produced by moving the clock. At the speed an aircraft travels these differences are measured in
millionths of a second, but they are real and in extremely close agreement with what special relativity says they should
be. You can read more about the time differences experienced by aircraft and the people on them here.
Despite being counter-intuitive the theory has passed every experimental test so far carried out on it.


Time dilation at 90% of the speed of light
90% of the speed of light
After travelling at 90% of the speed of light for 5 years the passengers of a
rocket returning home would find that around 10 Earth years had gone by:
0% of the speed of light



[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ]
[ Black Holes ] [ Twin Paradox ]
advertisement
Special relativity
advertisement

Introduction

Advertisement


The Special Theory of Relativity was proposed in 1905 by
Albert Einstein (1879 - 1955). The reason it is "special" is
because it is part of, or a "special case" of, the more
comprehensive and complex General Theory of Relativity. The
latter, General Theory, was proposed by Einstein in 1915.

Space and Time
In an everyday co-ordinate system, such as a map, it's possible
to specify a location using just dimensional distances. For
example, to someone looking for buried treasure we could say
"go east for 20 miles, north for 5 miles, then dig down 30 feet."
We have just specified a three dimensional co-ordinate system.
To this, Einstein added another factor, that of time. This still
makes sense in our everyday world: "go east for 20 miles, north
for 5 miles, dig down 30 feet, and then wait until 3 o'clock when
I will meet you to share the treasure!"
However, if we go at very high speeds, speeds close to the
speed of light, things begin to change in a very unexpected
way. The faster we go the more our clock slows down relative
to someone standing still; time, for anything moving, changes.
Instead of space and time being separate entities they are the
same thing, called space-time. In short: “moving clocks run
slow”.

Moving clocks run slow

The theory is based on two principles (postulates):
Physical laws are the same in all frames of reference.
That is; any event within a portion of space (a frame) can
be specified by three spatial dimensions (east-west, north-
south, up-down) and one temporal dimension (time). Also,
the laws that apply to us in everyday circumstances (such
as Newton's laws) also apply within each frame of
reference.
The speed of light is constant. That is, in a vacuum,
such as in space, the speed of light is always the same,
regardless of the speed of someone observing it.
The first postulate is seemingly simple and trivial. If I sit and
wait an hour in New York, an hour passes. If I sit and wait an
hour in London then an hour also passes. I am, almost exactly,
in the same bit of space (frame of reference), moving around
the Sun at the same speed wherever I sit on the Earth. The way
time passes in all frames of reference is governed by the same
laws.
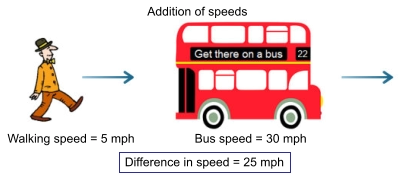
While the first postulate is pretty much what we might expect
the second requires a little more explanation. The speed of light
is very close to 300,000 kilometres per second (around 186,300
miles per second). Everyday experience tells us that if a bus is
moving north at 30 miles per hour and we are also walking
north at 5 miles per hour then the bus is moving away from us
at 25 miles per hour:
Einstein’s Two Postulates

But what if we move in the same direction as a light beam?
Let's say we produce a pulse of light into space by quickly
flashing a torch (flashlight) on and off. We then follow the beam
of light in a very fast rocket moving at 100,000 km per second.
How fast is the light beam moving away from us? Common
sense tells us that it's moving away from us 300,000 km minus
100,000 km per second. In other words, the light beam is
200,000 km per second faster than us. Wrong!
Remember that the speed of light is always the same
regardless of our own speed. From our rocket we would see
that the beam of light is still moving away from us at 300,000
km per second! Likewise, if we were moving towards the beam
at a very high speed we would still see the light coming at us at
300,000 km per second! This has enormous, but not always
obvious, implications.
If the speed of light stays the same then something else has to
change. That "something" is time.
As odd as it seems time is not constant. More accurately,
space-time is not constant. It can be changed, bent and twisted.
The faster we go the more time slows down ("moving clocks run
slow"), i.e. time becomes “dilated”. This is only really noticeable
at very high speeds such as those approaching the speed of
light; 300,000 km per second (186,300 miles per second), or
approximately 7 times around the Earth in a second.
One of the most dramatic consequences of space-time not
being constant is that time itself will run at different speeds as
measured by any clock, including own own body clocks. In
addition, a stationary clock will measure the passing of time at a
different rate to that of a moving clock, even if both clocks are
observed simultaneously. The clocks are each behaving
normally in their respective frames, but different to each other in
their relative frames, hence “relativity”.
The twin paradox
Time Dilation
Let's have an example. Mary, a 30 year old NASA astronaut,
blasts off in her very high speed rocket in the year 2050 on a 10
year mission to a nearby star. After a short time she is travelling
at 270,000 km per second, that is, 90% of the speed of light. To
Mary everything looks normal in her rocket; the clock seems
normal and time passes for her the way it did back on Earth.
Her identical twin sister, Susan, is a NASA ground controller for
the mission. Ten years pass on Earth before the rocket returns
and when it does so something is immediately apparent; while
the Earth-bound Susan has aged 10 years, her high-flying
"twin" sister has only aged 5 years! How can this be?
Well, again, we are back to "moving clocks run slow". At 90% of
the speed of light time slows down to about half of that relative
to someone who is stationary. So while 10 years have passed
for Susan only 5 years have passed for Mary because her
"clock" was running at half the speed of those on Earth. This is
called the twin paradox. Remember that while Mary has only
aged 5 years she still felt that time was passing normally, i.e. at
it’s usual rate. Not only was her clock running slow as far as any
ground based observers are concerned, but her time was
running slow.
One question that often crops up is why was it that Susan and
her rocket that experienced time dilation and not Mary? After
all, couldn’t we equally regard Susan as standing still and Mary
and the Earth as moving away from her?
The answer is that speeds can’t be achieved instantly and it is
the acceleration of one body of mass away from another that
determines which body of mass experiences the dilation.
Simple examples of this are found in atomic accelerators. For
example, the half-life of a free neutron is about 10 minutes.
That is, half of any neutrons will decay (fall apart) in about 10
minutes once unbound from other particles. However, if
accelerated to about 90% of the speed of light then the half-life
of the neutrons increases to about 15 minutes, i.e. just as
relativity dictates it should (their clocks are running slow).The
scientists watching and measuring this are stationary, relative
to the accelerated neutrons, and so they do not experience
dilation. In the same way, Susan accelerated away from Mary
and so she is the one who experienced time dilation. (There’s
a very good reason why the machines such as those at CERN
are called accelerators)

How Fast Can I Go?



Is It Real?
This is all well and good, but what evidence is there? After all
it's just a "theory". Some clarification is required here.
Unlike its use in the everyday world, scientists use the word
theory only when there is substantial and verifiable evidence for
an observed phenomena. In this sense a scientific theory is
quite unlike a conjecture or idea, and more often than not
requires a great deal of observational and experimental
evidence before attaining the status of theory. In the case of
special relativity there have been very many experiments
carried out and all of them have provided evidence that special
relativity is correct. These range from experiments involving
sub-atomic particles in high speed accelerators, as noted
earlier, to the slight, but expected, different clock rates of some
space exploration vehicles (such as the Voyager inter-planetary
probes) as compared with those on Earth. Even the GPS
satellites, which work by measuring time, have to take relativity
into account to stop their clocks quickly becoming
unsynchronised with those on Earth.
One example of supporting evidence for the theory is a much
simpler experiment that was first carried out in 1971 and has
been repeated many times since then. Atomic clocks have been
carried on aircraft making long flights such as over the Atlantic
ocean. An aircraft, even the fastest, goes at a tiny fraction of the
speed of light, but at any speed "moving clocks run slow". With
an atomic clock on the ground and one in the aircraft it's
possible to measure the tiny differences in time produced by
moving the clock. At the speed an aircraft travels these
differences are measured in millionths of a second, but they are
real and in extremely close agreement with what special
relativity says they should be. You can read more about the
time differences experienced by aircraft and the people on them
here.
Despite being counter-intuitive the theory has passed every
experimental test so far carried out on it.

Albert Einstein (1879 - 1955)

Time dilation at 90% of the speed of light
90% of the speed of light
After travelling at 90% of the speed of light for 5 years the passengers of a
rocket returning home would find that around 10 Earth years had gone by:
0% of the speed of light

Advertisement











