



Solving the Equation

Light, sound and water all travel as waves. The equation that describes this wave motion is the same for all three types
of wave. This is it:
The frequency, f, of a wave is the number of times a wave's crests pass a point in a second. If you watch a water wave in
the bath pass over one of your toes twice every second the frequency of the wave is 2 Hz. The unit "Hz" is short for hertz,
named after the German physicist Heinrich Hertz (1857 – 94). A more mathematically useful way to write 2 Hz is 2 s
–1
.
That is, "2 per second".
The speed of light has been given the letter c. In fact, as with all mathematical letters it is just a label and any letter would
do providing we state what we mean when we use it. The speed of light is close to 300,000 km/s (186,300 miles per
second). Another way of writing this is:
This means a three with eight zeros behind it, i.e. 300,000,000 metres per second.
The Greek letter lambda (λ), which looks like an upside-down letter y, is used to denote the wavelength of the wave. Again
this is just a label, or shorthand, in order to allow us to work quickly with the equation. Wavelengths are usually measured
in metres.
Providing that we know any two of the three quantities we can find the other one, either directly or by rearranging the
equation. The next section solves the equation as it is, and there is a calculator for frequency, wavelength and speed here.
In this example we will consider the frequency of radio waves. Radio waves are just another form of "light", i.e. part of the
electromagnetic spectrum, and so travel at the speed of light. Let's say we have a radio with a dial that is only marked in
MHz. This is a measurement of frequency and we note that 1 MHz is the same as 1 million hertz (the M in MHz stands for
"mega", which means million). We are told of a radio broadcast we want to hear but we are only given the wavelength of
the station and not the frequency. The wavelength we are given is 3.26 metres.
We know the speed of light and we know the wavelength so it's now an easy matter to plug these numbers into the
equation and find the frequency of the radio station:
This gives us a frequency of 92 MHz, which is found in the FM range of most domestic radios.
Visible Light
The wavelengths of visible light are measured in nanometres, nm (billionths of a metre) but the equation works just the
same. For example, red light has a wavelength of around 620 – 740 nm and blue light has a wavelength of around 445 –
500 nm. When we look at a light source the colours we see are dictated by the frequency of the light. These frequencies
are very high by everyday standards.
Have a look around the room and find something that's the colour red. How many times are the tiny crests of the light
waves coming from that red object passing through the front of your eyes every second? In other words, what is the
frequency of red light? Well, we know the speed of light and can take an average figure for the wavelength of red light.
Let's say it's 670 nm, that is:
We now have everything we need to work out the frequency:
So when we look at something that is medium red about 448,000,000,000,000 tiny little wave crests pass through our
eyes every second! This is certainly a very large number but still measurable using modern equipment. Indeed, the
screen you are using had to have this number taken into account when it was being designed. If it hadn't you wouldn't be
able to see this:
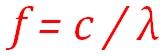



An Equation for all Waves
3 x 10
8
ms
-1

670 x 10
-9
m

Advertisement
speed frequency and wavelength



Light, sound and water all travel as waves. The equation that
describes this wave motion is the same for all three types of
wave. This is it:
The frequency, f, of a wave is the number of times a wave's
crests pass a point in a second. If you watch a water wave in
the bath pass over one of your toes twice every second the
frequency of the wave is 2 Hz. The unit "Hz" is short for hertz,
named after the German physicist Heinrich Hertz (1857 – 94).
A more mathematically useful way to write 2 Hz is 2 s
–1
. That
is, "2 per second".
The speed of light has been given the letter c. In fact, as with
all mathematical letters it is just a label and any letter would do
providing we state what we mean when we use it. The speed
of light is close to 300,000 km/s (186,300 miles per second).
Another way of writing this is:
This means a three with eight zeros behind it, i.e. 300,000,000
metres per second.
The Greek letter lambda, (λ) which looks like an upside-down
letter y, is used to denote the wavelength of the wave. Again this
is just a label, or shorthand, in order to allow us to work quickly
with the equation. Wavelengths are usually measured in metres.
Providing we know any two of the three quantities we can find
the other one, either directly or by rearranging the equation. The
next section solves the equation as it is, and there is a calculator
for frequency, wavelength and speed here.
Solving the Equation
In this example we will consider the frequency of radio waves.
Radio waves are just another form of "light", i.e. part of the
electromagnetic spectrum, and so travel at the speed of light.
Let's say we have a radio with a dial that is only marked in MHz.
This is a measurement of frequency and we note that 1 MHz is
the same as 1 million hertz (the M in MHz stands for "mega",
which means million). We are told of a radio broadcast we want
to hear but we are only given the wavelength of the station and
not the frequency. The wavelength we are given is 3.26 metres.
We know the speed of light and we know the wavelength so it's
now an easy matter to plug these numbers into the equation and
find the frequency of the radio station:
This gives us a frequency of 92 MHz, which is found in the FM
range of most domestic radios.

Visible Light
The wavelengths of visible light are measured in nanometres,
nm (billionths of a metre) but the equation works just the same.
For example, red light has a wavelength of around 620 – 740 nm
and blue light has a wavelength of around 445 – 500 nm. When
we look at a light source the colours we see are dictated by the
frequency of the light. These frequencies are very high by
everyday standards.
Have a look around the room and find something that's the
colour red. How many times are the tiny crests of the light waves
coming from that red object passing through the front of your
eyes every second? In other words, what is the frequency of red
light? Well, we know the speed of light and can take an average
figure for the wavelength of red light. Let's say it's 670 nm, that
is:
We now have everything we need to work out the frequency:
So when we look at something that is medium red about
448,000,000,000,000 tiny little wave crests pass through our
eyes every second! This is certainly a very large number but still
measurable using modern equipment. Indeed, the screen you
are using had to have this number taken into account when it
was being designed. If it hadn't you wouldn't be able to see this:
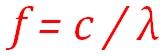
Finally in this section, you can quickly calculate frequency by
clicking on the box below. The calculator includes
rearrangements to make speed and wavelength the subject and
includes worked examples:


An Equation for all Waves

3 x 10
8
ms
-1
670 x 10
-9
m

Advertisement










