



Advertisement

The Light Clock
In other pages in this series we have seen that there is direct and measurable evidence for time dilation. One example
from the many available, that of atomic clocks carried on aircraft, has shown that moving clocks do indeed run more
slowly than stationary ones, just as predicted by Einstein’s equations.
The distinction between scientific "proof" and "evidence" is a complex one. For the moment though it is sufficient to say
that scientific proof is only available in models, and never in reality. The primary laboratory of the theoretical physicist is
his or her own mind and so it's there that any initial experiments must take place. These experiments are often called
"thought experiments". Of course, as Einstein was happy to admit, the only real way to test a theory is by carrying out
experiments in reality. However, the germ of any physical experiment must start in the mind, and this page looks at one
of the best examples of a such a thought experiment; that of the theoretical light clock.
The mind – Einstein’s laboratory
Clocks exist in many forms. Among the many types of clocks that have been made there are:
Water wheel clocks that collect water in buckets marked with time scales.
Candles with marks on them to show how long they have been burning.
Sundials that project the Sun's shadow onto graduated clock faces.
Clockwork clocks that gradually release the energy stored in wound springs.
Clocks that measure the vibrational frequency of crystals such as quartz, or even atoms.
Most clocks measure how many times a repetitive action is carried out. For example, in a digital watch the quartz crystal
usually vibrates at 32,768 times a second. These vibrations are counted by electronic circuits, and after 32,768 "ticks"
have been counted a second is added to the watch's display.





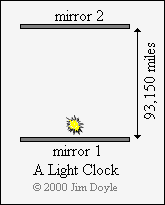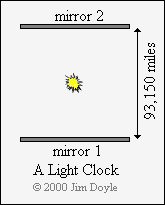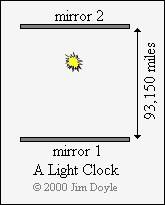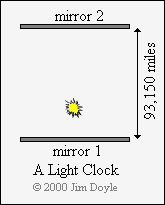
We can also use light to make a clock, at least in theory. To do this we need to bounce a pulse of light between two
mirrors that are a known distance apart. Light travels at 186,300 miles per second (very close to 300,000 km per
second), so if we separate the mirrors by a distance of 93,150 miles (i.e. half 186,300) each individual mirror will be
struck by the pulse of light once a second. In other words, the round trip from one mirror to the other and back again
will take the light pulse one second. We now have a clock:
There are a number of practical problems with such a clock. Probably the most obvious one is the separation distance of
the mirrors, but in reality we could put them very close together and count faster "ticks". The large separation used here
is just to demonstrate the principle and make the mathematics easier. In reality the mirrors would absorb some of the
light each time they were struck by the pulse and after a time the light pulse would dissipate completely. Also, the fact
that we can see the light at all means that at least some of it is being scattered, thereby further weakening the pulse.
None of this really matters however, because we are dealing with a theoretical proof and not an experimental one.
As an aside, there are systems that use the principle of a light clock in order to perform important tasks. Radar is
probably the best known example. In a radar system pulses of "light" (i.e. electromagnetic radiation) are beamed out at
very close to the speed of light. If the beam hits an object some of it will be reflected back (as if from a mirror) and can
then be detected by the radar receiver equipment. The time taken between the beam being emitted and re-absorbed can
be used to calculate the distance of the reflecting object, such as an aircraft.
Radar
The light clock in action
A Moving Light Clock and Pythagoras
There's nothing really that extraordinary about a stationary light clock. In fact, there's nothing really that extraordinary
about a moving light clock if we are on the same moving platform as it. Imagine being on a rocket moving at half the
speed of light and that on this rocket we have a light clock. As we travel through space we can see the clock ticking
away quite happily and there wouldn't be anything odd about it (okay, we have to use our imagination here because the
clock, as we have seen, would either be enormous or so small that we can't actually see the pulses, but, again, we must
remember that this is a thought experiment).
Now let's imagine that we're being watched by an external, and stationary, observer. We whiz past the observer while
holding the light clock to the window. Will we both see the light clock doing the same thing? No! To us on our rocket the
pulses of light just go up and down the way we would expect them to, but to the observer they will follow a different path,
one that maps out a series of triangles. The animation below shows the track of the light pulse as it moves past the
observer:
At first this may not seem so strange. After all we could do the same
experiment with anything that went up and down in a transparent box, but
this is light and light has some very strange properties. From the other
pages in this series we know that light has a constant speed, and this is
where things start to become interesting!
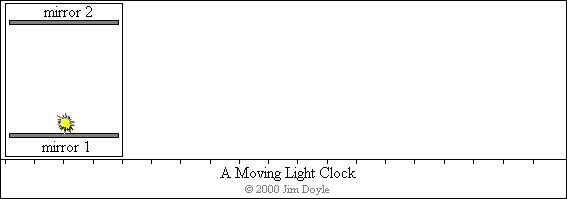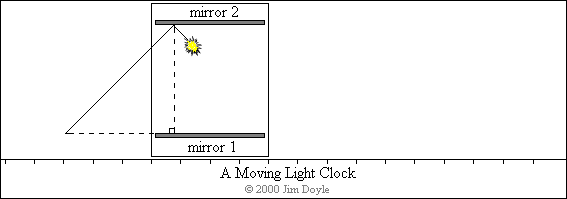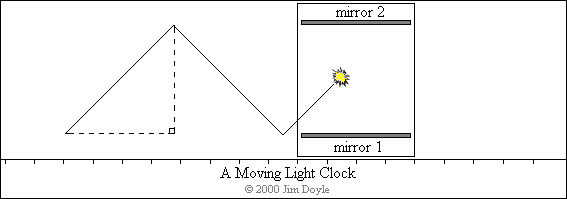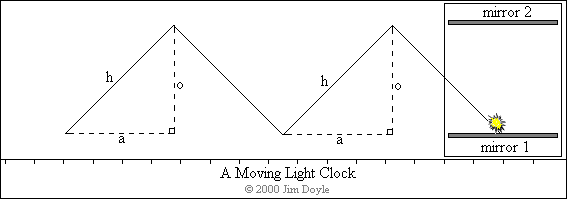
As we have seen, the light moves in such a way, as viewed by the external
observer, that it traces out a series of triangles. We know the mirrors are
separated by the distance that light travels in half a second (i.e. 93,150
miles) and that the spaceship is travelling at half the speed of light and so
covers 46,575 miles during the same time interval, i.e. half a second:

The mathematics are correct but the actual result is wrong! If it was correct it would mean that the pulse of light was
travelling a total distance of 2 x 104,145 miles = 208,290 miles per second. It's a pulse of light, however, and can’t travel
faster than 186,300 miles in a single second, nothing can!
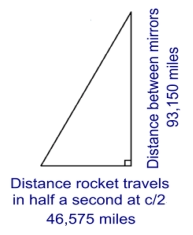
We have the opposite and adjacent measurements of a right-angled triangle
and all we need now is a little help from Pythagoras to work out the length of
the hypotenuse:

What’s going on?
The external observer knows that the distance tracked out by the pulse of light in a single second can't be more than
186,300 miles. He also knows that the speed of light is constant. If the speed of light can't change is there anything else
that can? Einstein pondered this problem and came to a breathtaking conclusion; if the speed of light is constant then it
must be space and time that change.
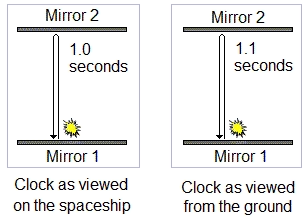
Einstein realised that what the external observer would really see would be a light clock that appears to be slowed down.
The clock has to behave in this way otherwise it would break the universal speed limit. The "ticks" of the clock would now
appear to be slower as viewed by the external observer than as viewed by the person on the rocket. The rocket is
moving at 50% of the speed of light so according to the external observer the time the pulse takes to get to the top mirror
and back again would be about 1.1 seconds. As viewed from an external stationary position the rocket, and everything
on it, would be running in slow motion. Time on the rocket has, according to the external observer, slowed down by
about 10%. To the person on the rocket however, time would still seem to be passing normally.
Not only that but the spaceship and all its contents, including the light clock, would appear to be contracted in the
direction of motion according to the external observer, but normal for the person on the spaceship. Again, this is a
consequence of the speed of light being constant and so forcing space (more accurately space-time) to shrink. If the
space traveller takes a ruler and measures something the results will appear normal because the ruler has shrunk as
well.
The two observers would be experiencing space and time in different ways relative to each other. Note that in each
individual's frame of reference everything seems normal; they would both feel time passing normally and the laws of
physics would still be the same (as the first postulate states). It's only when observing each other's frame of reference
that they notice anything strange. As the speed of light is approached these effects become ever more apparent:
A clock at 0% of
the speed of light
The same clock at 90% of
the speed of light
Summary
We have seen that due to the constant speed of light a moving light clock will appear to run slowly according to an
external observer. It was stated at the start of the page that the light clock was a thought experiment, and so it is.
However, not only is the light clock experiment expected to work in reality but every clock that has ever been observed at
high speeds slows down in just the way that the Special Theory of Relativity says it should. It's not just light clocks that
run slowly at high speeds, all clocks, including our own body clocks, slow down at high speeds. Time, for anything
moving, changes.
The light clock – A thought experiment
A Theoretical Proof
Advertisement
The light clock
Advertisement



NEW! Quick and Easy SuperFast Guides NEW!
[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ]
[ Black Holes ] [ Twin Paradox ] [ Time Dilation Formula ]
NEW! Quick and Easy SuperFast Guides NEW!
[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ]
[ Black Holes ] [ Twin Paradox ] [ Time Dilation Formula ]


Advertisement


In other pages in this series we have seen that there is direct and
measurable evidence for time dilation. One example from the
many available, that of atomic clocks carried on aircraft, has
shown that moving clocks do indeed run more slowly than
stationary ones, just as predicted by Einstein’s equations.
The distinction between scientific "proof" and "evidence" is a
complex one. For the moment though it is sufficient to say that
scientific proof is only available in models, and never in reality.
The primary laboratory of the theoretical physicist is his or her
own mind and so it's there that any initial experiments must take
place. These experiments are often called "thought
experiments". Of course, as Einstein was happy to admit, the
only real way to test a theory is by carrying out experiments in
reality. However, the germ of any physical experiment must start
in the mind, and this page looks at one of the best examples of a
such a thought experiment; that of the theoretical light clock.

The mind – Einstein’s laboratory
The Light Clock





Clocks exist in many forms. Among the many types of clocks
that have been made there are:
Water wheel clocks that collect water in buckets marked
with time scales.
Candles with marks on them to show how long they have
been burning.
Sundials that project the Sun's shadow onto graduated
clock faces.
Clockwork clocks that gradually release the energy stored
in wound springs.
Clocks that measure the vibrational frequency of crystals
such as quartz, or even atoms.
Most clocks measure how many times a repetitive action is
carried out. For example, in a digital watch the quartz crystal
usually vibrates at 32,768 times a second. These vibrations are
counted by electronic circuits, and after 32,768 "ticks" have
been counted a second is added to the watch's display.

We can also use light to make a clock, at least in theory. To do
this we need to bounce a pulse of light between two mirrors that
are a known distance apart. Light travels at 186,300 miles per
second (very close to 300,000 km per second), so if we separate
the mirrors by a distance of 93,150 miles (i.e. half 186,300) each
individual mirror will be struck by the pulse of light once a
second. In other words, the round trip from one mirror to the
other and back again will take the light pulse one second. We
now have a clock:
There are a number of practical problems with such a clock.
Probably the most obvious one is the separation distance of the
mirrors, but in reality we could put them very close together and
count faster "ticks". The large separation used here is just to
demonstrate the principle and make the mathematics easier. In
reality the mirrors would absorb some of the light each time they
were struck by the pulse and after a time the light pulse would
dissipate completely. Also, the fact that we can see the light at all
means that at least some of it is being scattered, thereby further
weakening the pulse. None of this really matters however,
because we are dealing with a theoretical proof and not an
experimental one.
As an aside, there are systems that use the principle of a light
clock in order to perform important tasks. Radar is probably the
best known example. In a radar system pulses of "light" (i.e.
electromagnetic radiation) are beamed out at very close to the
speed of light. If the beam hits an object some of it will be
reflected back (as if from a mirror) and can then be detected by
the radar receiver equipment. The time taken between the beam
being emitted and re-absorbed can be used to calculate the
distance of the reflecting object, such as an aircraft.

Radar
The light clock in action
A Moving Light Clock and Pythagoras
There's nothing really that extraordinary about a stationary light
clock. In fact, there's nothing really that extraordinary about a
moving light clock if we are on the same moving platform as it.
Imagine being on a rocket moving at half the speed of light and
that on this rocket we have a light clock. As we travel through
space we can see the clock ticking away quite happily and there
wouldn't be anything odd about it (okay, we have to use our
imagination here because the clock, as we have seen, would
either be enormous or so small that we can't actually see the
pulses, but, again, we must remember that this is a thought
experiment).
Now let's imagine that we're being watched by an external, and
stationary, observer. We whiz past the observer while holding
the light clock to the window. Will we both see the light clock
doing the same thing? No! To us on our rocket the pulses of
light just go up and down the way we would expect them to, but
to the observer they will follow a different path, one that maps
out a series of triangles. The animation below shows the track of
the light pulse as it moves past the observer:

At first this may not seem so strange. After all we could do the
same experiment with anything that went up and down in a
transparent box, but this is light and light has some very strange
properties. From the other pages in this series we know that
light has a constant speed, and this is where things start to
become interesting!
As we have seen, the light moves in such a way, as viewed by
the external observer, that it traces out a series of triangles. We
know the mirrors are separated by the distance that light travels
in half a second (i.e. 93,150 miles) and that the spaceship is
travelling at half the speed of light and so covers 46,575 miles
during the same time interval, i.e. half a second:
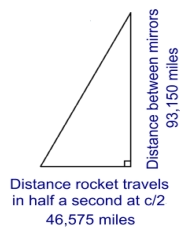
We have the opposite and adjacent measurements of a right-
angled triangle and all we need now is a little help from
Pythagoras to work out the length of the hypotenuse:

The mathematics are correct but the actual result is wrong! If it
was correct it would mean that the pulse of light was travelling a
total distance of 2 x 104,145 miles = 208,290 miles per second.
It's a pulse of light, however, and can’t travel faster than 186,300
miles in a single second, nothing can!
What’s going on?

The external observer knows that the distance tracked out by the
pulse of light in a single second can't be more than 186,300
miles. He also knows that the speed of light is constant. If the
speed of light can't change is there anything else that can?
Einstein pondered this problem and came to a breathtaking
conclusion; if the speed of light is constant it then must be space
and time that change.
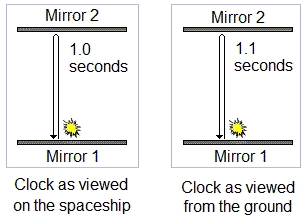
Einstein realised that what the external observer would really see
would be a light clock that appears to be slowed down. The clock
has to behave in this way otherwise it would break the universal
speed limit. The "ticks" of the clock would now appear to be
slower as viewed by the external observer than as viewed by the
person on the rocket. The rocket is moving at 50% of the speed
of light so according to the external observer the time the pulse
takes to get to the top mirror and back again would be about 1.1
seconds. As viewed from an external stationary position the
rocket, and everything on it, would be running in slow motion.
Time on the rocket has, according to the external observer,
slowed down by about 10%. To the person on the rocket
however, time would still seem to be passing normally.
Not only that but the spaceship and all its contents, including the
light clock, would appear to be contracted in the direction of
motion according to the external observer, but normal for the
person on the spaceship. Again, this is a consequence of the
speed of light being constant and so forcing space (more
accurately space-time) to shrink. If the space traveller takes a
ruler and measures something the results will appear normal
because the ruler has shrunk as well.
The two observers would be experiencing space and time in
different ways relative to each other. Note that in each
individual's frame of reference everything seems normal; they
would both feel time passing normally and the laws of physics
would still be the same (as the first postulate states). It's only
when observing each other's frame of reference that they notice
anything strange. As the speed of light is approached these
effects become ever more apparent:
A clock at 0% of
the speed of light
The same clock at 90% of
the speed of light
Summary
We have seen that due to the constant speed of light a moving
light clock will appear to run slowly according to an external
observer. It was stated at the start of the page that the light clock
was a thought experiment, and so it is. However, not only is the
light clock experiment expected to work in reality but every clock
that has ever been observed at high speeds slows down in just
the way that the Special Theory of Relativity says it should. It's
not just light clocks that run slowly at high speeds, all clocks,
including our own body clocks, slow down at high speeds. Time,
for anything moving, changes.

The light clock – A thought experiment
A Theoretical Proof

The Light Clock
A Theoretical Proof of
Time Dilation



NEW! Quick and Easy SuperFast Guides NEW!
[ Time Dilation Formula ] [ General Relativity ] [ Einstein ]
[ Time Dilation ] [ Black Holes ] [ Twin Paradox ]









