
The time dilation equation



Of all the major advances in physics from about 1900 onwards Special Relativity is the only one that can be reasonably
well understood in its entirety without recourse to mathematics beyond that of high school level. However, just as with all
physics, special relativity has at its base a precise set of mathematical formulas from which predictions can be made and
tested against experimental results. It will come as no surprise then that time dilation also has a precise mathematical
formula. This is it:
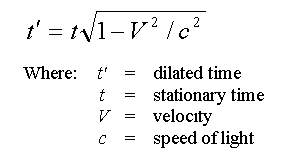
Example 1: Solving the equation as a factor of 1
Let’s look now at a couple of examples of how to solve the equation.
The effects of time dilation don't become really noticeable until very high speeds are reached so for this worked example
I will use a speed of 90% of that of light, that is 270,000 km per second (the speed of light is very close to 300,000 km
per second, or 186,300 miles per second). The first thing we must do is to write down the equation:
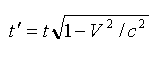
We now need to "plug in the numbers". Because V
2
/ c
2
is a ratio we can either use the exact values or just the
percentages of each value. It's easier, in this case, to do the latter. Because we're only interested in the dilated time
factor we can set the stationary time to be 1. Note that we can drop the percentage symbols and that c is equal to 100%
of the speed of light. Plugging in the numbers we get:
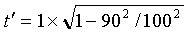
We can now begin to solve the equation. The first thing we can do is
remove the leading number 1 (anything multiplied by 1 is itself), then
square the last two terms:
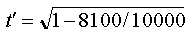
We can now reduce the equation by carrying out the division:
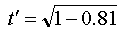
We then carry out the subtraction:
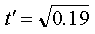
And finally we take the square root (and round the answer to a
workable value):
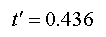
This result means that at 90% of the speed of light local time has slowed down to 43.6% of that relative to an external
observer. Put another way, if a rocket is sent out into space on a 10 (Earth) year mission at 90% of the speed of light the
rocket and its occupants will have only aged by about four and a half years when they return, while everyone and
everything on Earth will have aged 10 years. You can read more about this “twin paradox” on this page.
Example 2: Solving the equation as a measure of time
The first example solved the equation as a factor of 1. This example puts a real time scale into the equation. In this
example we will look at how time changes over 10 years travelling at a speed of 50% of that of light.
Instead of the commentary approach of the last example I will just carry out the equation but show each of the steps
involved (this equation can also be automatically calculated by clicking here or on the link below):
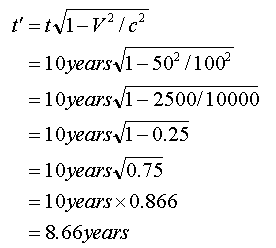
So for a rocket travelling at 50% of the speed of light 8.66 years will pass in the same time as 10 years pass for a
stationary observer. Note that while the unit of time used was years it could have been any other unit of time, such as
seconds or millennia, as long as the result is in the same units as the units used in the equation.
As a side note, something that is only rarely, if ever, mentioned in science fiction is the effects of time dilation. Instead,
we see spaceships travelling for months or even years on end and then returning to Earth with no differences in time. If
we ever do manage to send people into space at very high percentages of the speed of light there will be the added
dimension of different rates of ageing. For example, it would be possible for astronauts to return only to find that their
children are older than they are. There’s also the question of whether or not they are to be paid in ship time or Earth time!
A final point is that the equation holds for all speeds, even the speeds we move about at from day to day, such as when
walking, driving or flying. You can read more about this and see how much time you “gain” in such low speed travel here.


Advertisement
Time dilation worked examples

Time Dilation
Worked Examples





The time dilation equation
Of all the major advances in physics from about 1900 onwards
Special Relativity is the only one that can be reasonably well
understood in its entirety without recourse to mathematics
beyond that of high school level. However, just as with all
physics, special relativity has at its base a precise set of
mathematical formulas from which predictions can be made and
tested against experimental results. It will come as no surprise
then that time dilation also has a precise mathematical formula.
This is it:
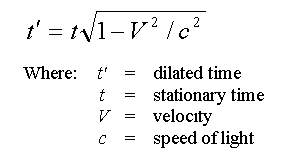
Let’s look now at a couple of examples of how to solve the
equation.
Example 1: Solving the equation as a factor of 1
The effects of time dilation don't become really noticeable until
very high speeds are reached so for this worked example I will
use a speed of 90% of that of light, that is 270,000 km per
second (the speed of light is very close to 300,000 km per
second, or 186,300 miles per second). The first thing we must
do is to write down the equation:
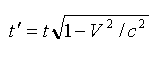
We now need to "plug in the numbers". Because V
2
/ c
2
is a
ratio we can either use the exact values or just the percentages
of each value. It's easier, in this case, to do the latter. Because
we're only interested in the dilated time factor we can set the
stationary time to be 1. Note that we can drop the percentage
symbols and that c is equal to 100% of the speed of light.
Plugging in the numbers we get:
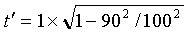
We can now begin to solve the equation. The first thing we can
do is remove the leading number 1 (anything multiplied by 1 is
itself), then square the last two terms:
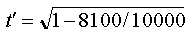
We can now reduce the equation by carrying out the division:
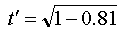
We then carry out the subtraction:
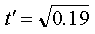
And finally we take the square root (and round the answer to a
workable value):
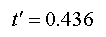
This result means that at 90% of the speed of light local time
has slowed down to 43.6% of that relative to an external
observer. Put another way, if a rocket is sent out into space on a
10 (Earth) year mission at 90% of the speed of light the rocket
and its occupants will have only aged by about four and a half
years when they return, while everyone and everything on Earth
will have aged 10 years. You can read more about this “twin
paradox” on this page.
Example 2: Solving the equation as a measure of time
The first example solved the equation as a factor of 1. This
example puts a real time scale into the equation. In this example
we will look at how time changes over 10 years travelling at a
speed of 50% of that of light.
Instead of the commentary approach of the last example I will
just carry out the equation but show each of the steps involved:
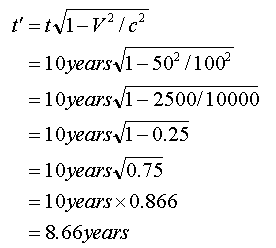
So for a rocket travelling at 50% of the speed of light 8.66 years
will pass in the same time as 10 years pass for a stationary
observer. Note that while the unit of time used was years it could
have been any other unit of time, such as seconds or millennia,
as long as the result is in the same units as the units used in the
equation. A calculator for this equation is also provided here.
As a side note, something that is only rarely, if ever, mentioned
in science fiction is the effects of time dilation. Instead, we see
spaceships travelling for months or even years on end and then
returning to Earth with no differences in time. If we ever do
manage to send people into space at very high percentages of
the speed of light there will be the added dimension of different
rates of ageing. For example, it would be possible for astronauts
to return only to find that their children are older than they are.
There’s also the question of whether or not they are to be paid in
ship time or Earth time!
A final point is that the equation holds for all speeds, even the
speeds we move about at from day to day, such as when
walking, driving or flying. You can read more about this and see
how much time you “gain” in such low speed travel here.


Advertisement
Advertisement

Time Dilation
Worked Examples










