
The speed of time


Advertisement

One of the consequences of Special Relativity is that any moving clock slows down in accordance with a precise
mathematical formula. The faster the clock is moving the more it slows down. The clock slows down for a very good
reason; time itself, for anything moving, slows down relative to a stationary observer. This idea was put forward in 1905
by Albert Einstein and has since been tested many times. In particular, the accuracy of very precise atomic clocks has
allowed us to verify the effects of time dilation at even very modest speeds.
This page gives examples of how time is slowed down at a variety of speeds, but concentrates on speeds that we can
encounter as a matter of routine. The effects of time dilation only start to become apparent at speeds close to the speed
of light (300,000 km per second, or 186,300 miles per second). For more detailed information on time dilation see this
page, and you can find a time dilation calculator here.
A table of time
At the speeds we travel at in everyday life time dilation is so small that it's not detectable to all but atomic clocks. Even if
you were to spend your whole life travelling in a fast modern jet your time dilation as measured by a stationary observer
would still not even register on a digital watch, as we will see later in this page.
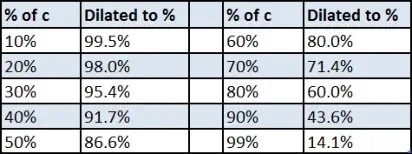
While the equation dealing with time dilation isn't especially difficult, it's perhaps more instructive to see some of the
results listed as a table such as in the one below. Here we see the percentage of the speed of light (c) against its dilated
percentage, so that, for example, travelling at 90% of the speed of light time results in time slowing down to 43.6% of its
usual rate:
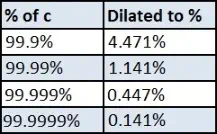
From the table it’s easy to see that time is only altered a little until we get to speeds above about 50% of that of light, and
then the effect becomes ever more dramatic. Beyond 99% of the speed of light time slows down very rapidly indeed, as
shown here:
So as we get ever closer to the speed of light time slows down until it almost stops. However, note that it’s not possible to
reach 100% of the speed of light (as explained on this page) and so time never quite comes to a complete standstill.
You can experiment with different percentages of by light using the Time Dilation Calculator here, all the way up to
99.99999999999999% of the speed of light.

Example 1: A flight over the Atlantic
Now let’s look at a some examples of dilation at relatively low speeds.
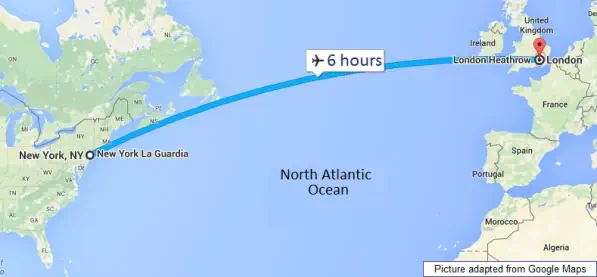
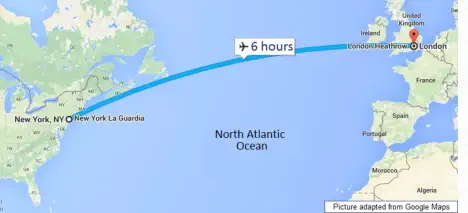
For most of us the biggest and longest time dilation we ever experience is on a long flight, such as over the Atlantic
Ocean. Such a flight takes about six hours and the average speed is about 550 mph (880 km/h). Now, 550 mph is
undoubtedly very fast in human terms but the only change we have to make to a watch at the end of such a flight is to
adjust it to the local time, and we don't need to alter it to take time dilation into account. Does this mean there is no time
dilation during the flight? No! It's just that the time dilation, even at the speed of a jet, is so small that our everyday
watches can't measure it. Remember, all moving clocks run slowly, even slowly moving ones.
Six hours at 550 mph (880 km/h). Time dilation?
So how much time do we "save" on such a flight? To answer this we must first convert hours into seconds and miles per
hour into metres per second. When we do this we get:
6 hours = 21,600 seconds
550 mph = 244 metres per second
The next thing we need to do is to "plug" these numbers into the time dilation equation and carry out the calculation. In
doing so I will use a form of the equation that can be written more easily using a word processor (the results are exactly
the same as using the more usual format of the equation and can be checked here):
![dilated time = initial time x (1 – V^2/c^2)^(1/2) = 21600 x [1 – (244 ms^-1)^2 / (3 x 10^8 ms^-1)^2]^(1/2) = 21600 x 0.999 999 999 999 7 = 21599.999 999 99 s](index_htm_files/2677.webp)
So how much time has been saved? In other words, by how much has time been dilated? To answer this we simply
subtract the dilated time from the time as observed by a stationary observer:
21600s – 21599.999 999 99 s = 0.000 000 1 seconds
This is a tiny amount of time! Can this prediction be checked? Amazingly, yes it can, using atomic clocks.
Atomic clocks work by monitoring the natural vibrational frequency of atoms and are very accurate. In 1971 two scientists,
J. Hafele and R Keating, borrowed four atomic clocks from the U.S. Naval Observatory, put them on commercial airliners
and flew them around the world. When compared with similar atomic clocks back in the U.S. they found that the clocks
slowed down by the tiny, but very real amount predicted by Einstein’s time dilation equations. This experiment has since
been carried out many times using ever more accurate atomic clocks. Each time the results have been in accordance
with what Einstein said they would be. Time dilation, even at low speeds, is real.

Example 2: The lifetime of a pilot
In the previous example we looked at a single flight over the Atlantic Ocean and found that the time difference was very
small. What happens, however, if we spend a large part of our lives making such journeys. Surely the time dilations all
add up and we can live longer! This is only half true and depends on an individual's "frame of reference". In the first place
anyone making such journeys would still feel time passing normally, so they may live longer according to an external
observer but would still experience time passing the way everyone else does. In the second place, as we shall see, the
amount of time "saved" is still very tiny.
Do aircrew live longer?
For this example we will look at an airline pilot. For simplicity let's say that our pilot spends his or her whole career on the
Atlantic route, flying (on average) 25 hours a week for 40 years at an average speed of 550 mph (880 km/h). This is
undoubtedly a lot of "high" speed travelling but how much time will our pilot "save" due to time dilation?
As in the previous example we must first convert the figures we have into more suitable units:
25 hours x 40 years = 52,000 hours
550 mph = 244 metres per second
Note that we didn't have to convert the hours into seconds. Using hours will work just as well and our initial answer will
also be in hours. Plugging these numbers into the time dilation equation gives us an answer of:
dilated time = initial time x (1 – V^2/c^2)^(1/2)
= 52000 hours x [1 – (244 ms^-1)^2 / (3 x 10^8 ms^-1)^2]^(1/2)
= 52000 hours x 0.999 999 999 999 7
= 51599.999 999 984 4 hours
Subtracting this value from the value measured by an external observer gives us a total time "saved" of:
52000 hours – 51599.999 999 984 4 hours = 0.000 000 015 6 hours
This is perhaps better expressed as seconds, in which case we find that in a lifetime of flying our airline pilot saves a total
of 0.000056 seconds as compared to an external observer. Again, this is measurable by atomic clocks, but not in the
least bit noticeable to the pilot or anyone else. There must be a better way! Let's try going even faster and for much
longer...
Example 3: The Voyager Project
In 1977 two remarkable spacecraft were launched by NASA, they were called Voyager 1 and Voyager 2. During the
following decade these two small probes visited the largest planets in our Solar System and provided spectacular and
breathtaking information about our local neighbourhood. Although expected to function and send back data until at least
the late 2020s they have both long since left our planetary system and are heading out into deep space where, it is
tentatively hoped, they may one day many millions of years from now be found by other inhabitants of our galaxy.
Just in case they're found "gramophone" records have been attached to each spacecraft. These records contain
information about us. Each contains greetings in many languages, such as English, Hindi and even Latin. They can also
play music from many cultures, including everything from Bach to Australian Aborigine songs. A map has also been
supplied. It tells anyone that finds it where we are and "when" we are. We have been beaming signals into space since at
least the invention of television, but this is our first intentional solid message. If there really is someone out there we might
just be able to say hello.

The Voyager Golden Record -- A greeting from Planet Earth
One of the most notable things about the two Voyager spacecraft is their speed. Voyager 1 is travelling at around 35,500
mph (57,500 km/h) and this is the craft we will concentrate on. The Earth is about 24,000 miles in circumference and so it
would take much less than an hour for Voyager 1 to circumnavigate the whole planet. The fastest speed that a human
being has so far travelled is during the journey to the Moon and back. To get to the Moon took about three days. For
Voyager 1 it would take only seven hours.
Apart from the Sun, the nearest star to us is Alpha Proxima. This faint star is about 4.37 light years away from us. That is,
travelling at 186,300 miles per second it would take 4.37 years to get there (as measured by Earth clocks!). At the speed
Voyager 1 is travelling it would reach our nearest stellar neighbour in about 80,000 years. What would be the time dilation
experienced? In other words, travelling at the speed it is how much younger will Voyager 1 be than an Earth-bound
observer 80,000 years from now?
In this case we will use the actual speed as opposed to the percentage of the speed of light that we have used before.
This makes no difference to the calculations as long as we make sure that the units are the same, i.e. either both as an
absolute speed or both as a percentage. As always, we have to convert the units to something we can easily work with:
Voyager 1 = 35,000 mph
= 57,000 km/h
= 16,000 metres per second
(about 10 miles a second)
We know the (stationary) time is 80,000 years so now we have all the information we need to solve the time dilation
equation:
![dilated time = initial time x (1 – V^2/c^2)^(1/2) = 80000 years x [1 – (16000 ms^-1)^2 / (3 x 10^8 ms^-1)^2]^(1/2) = 80000 years x (0.9999999971556)^1/2 = 80000 years x 0.9999999985778 = 79999.99988622 years](index_htm_files/2896.webp)
We now subtract the measured time according to an external observer:
80000 years – 79999.99988622 years = 0.00011378 years
If we convert this to a more convenient time scale we find that it is just under one hour. After 80,000 years travelling
through space at 35,500 mph Voyager 1 will be only about one hour "younger" than the Earth! In comparison to the
speed of light Voyager 1, for all its outstanding contributions to the understanding of our Solar System, is very, very slow.
So slow in fact that it's possible that our distant descendants could intercept the craft before any alien civilisation gets the
chance. In fact, Voyager 1 could turn out to be biggest find in the archaeology of the distant future. Personally, I hope it's
left to go on its way.

Voyager -- Earth’s messenger

Advertisement
[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ]
[ Black Holes ] [ Twin Paradox ]
Time dilation at low speeds





The speed of time
One of the consequences of special relativity is that any moving
clock slows down in accordance with a precise mathematical
formula. The faster the clock is moving the more it slows down.
The clock slows down for a very good reason; time itself, for
anything moving, slows down relative to a stationary observer.
This idea was put forward in 1905 by Albert Einstein and has
since been tested many times. In particular, the accuracy of very
precise atomic clocks has allowed us to verify the effects of time
dilation at even very modest speeds.
This page gives examples of how time is slowed down at a
variety of speeds, but concentrates on speeds that we can
encounter as a matter of routine. The effects of time dilation only
start to become apparent at speeds close to the speed of light
(300,000 km per second, or 186,300 miles per second). For
more detailed information on time dilation see this page, and
you can find a time dilation calculator here.
A table of time

From the table it’s easy to see
that time is only altered a little
until we get to speeds above
about 50% of that of light, and
then the effect becomes ever
more dramatic. Beyond 99% of
the speed of light time slows
down very rapidly indeed, as
shown here:

So as we get ever closer to the speed of light time slows down
until it almost stops. However, note that it’s not possible to reach
100% of the speed of light (as explained on this page) and so
time never quite comes to a complete standstill.
You can experiment with different percentages of by light using
the Time Dilation Calculator here, all the way up to
99.99999999999999% of the speed of light.
Example 1: A flight over the Atlantic
Now let’s look at a some examples of dilation at relatively low
speeds.
For most of us the biggest and longest time dilation we ever
experience is on a long flight, such as over the Atlantic Ocean.
Such a flight takes about six hours and the average speed is
about 550 mph (880 km/h). Now, 550 mph is undoubtedly very
fast in human terms but the only change we have to make to a
watch at the end of such a flight is to adjust it to the local time,
and we don't need to alter it to take time dilation into account.
Does this mean there is no time dilation during the flight? No! It's
just that the time dilation, even at the speed of a jet, is so small
that our everyday watches can't measure it. Remember, all
moving clocks run slowly, even slowly moving ones.
Six hours at 550 mph (880 km/h). Time dilation?
So how much time do we "save" on such a flight? To answer this
we must first convert hours into seconds and miles per hour into
metres per second. When we do this we get:
6 hours = 21,600 seconds
550 mph = 244 metres per second
The next thing we need to do is to "plug" these numbers into the
time dilation equation and carry out the calculation. In doing so I
will use a form of the equation that can be written more easily
using a word processor (the results are exactly the same as
using the more usual format of the equation and can be checked
here):
![dilated time = initial time x (1 – V^2/c^2)^(1/2) = 21600 x [1 – (244 ms^-1)^2 / (3 x 10^8 ms^-1)^2]^(1/2) = 21600 x 0.999 999 999 999 7 = 21599.999 999 99 s](index_htm_files/2706.webp)
So how much time has been saved? In other words, by how
much has time been dilated? To answer this we simply subtract
the dilated time from the time as observed by a stationary
observer:
21600s – 21599.999 999 99 s = 0.000 000 1 seconds
This is a tiny amount of time! Can this prediction be checked?
Amazingly, yes it can, using atomic clocks.
Atomic clocks work by monitoring the natural vibrational
frequency of atoms and are very accurate. In 1971 two
scientists, J. Hafele and R Keating, borrowed four atomic clocks
from the U.S. Naval Observatory, put them on commercial
airliners and flew them around the world. When compared with
similar atomic clocks back in the U.S. they found that the clocks
slowed down by the tiny, but very real amount predicted by
Einstein’s time dilation equations. This experiment has since
been carried out many times using ever more accurate atomic
clocks. Each time the results have been in accordance with what
Einstein said they would be. Time dilation, even at low speeds,
is real.

In the previous example we looked at a single flight over the
Atlantic Ocean and found that the time difference was very
small. What happens, however, if we spend a large part of our
lives making such journeys. Surely the time dilations all add up
and we can live longer! This is only half true and depends on an
individual's "frame of reference". In the first place anyone
making such journeys would still feel time passing normally, so
they may live longer according to an external observer but would
still experience time passing the way everyone else does. In the
second place, as we shall see, the amount of time "saved" is still
very tiny.
Do aircrew live longer?
Example 2: The lifetime of a pilot
For this example we will look at an airline pilot. For simplicity
let's say that our pilot spends his or her whole career on the
Atlantic route, flying (on average) 25 hours a week for 40 years
at an average speed of 550 mph (880 km/h). This is
undoubtedly a lot of "high" speed travelling but how much time
will our pilot "save" due to time dilation?
As in the previous example we must first convert the figures we
have into more suitable units:
25 hours x 40 years = 52,000 hours
550 mph = 244 metres per second
Note that we didn't have to convert the hours into seconds.
Using hours will work just as well and our initial answer will also
be in hours. Plugging these numbers into the time dilation
equation gives us an answer of:
dilated time = initial time x (1 – V^2/c^2)^(1/2)
= 52000 hours x [1 – (244 ms^-1)^2 / (3 x 10^8 ms^-1)^2]^(1/2)
= 52000 hours x 0.999 999 999 999 7
= 51599.999 999 984 4 hours
Subtracting this value from the value measured by an external
observer gives us a total time "saved" of:
52000 hours – 51599.999 999 984 4 hours = 0.000 000 015 6 hours
This is perhaps better expressed as seconds, in which case we
find that in a lifetime of flying our airline pilot saves a total of
0.000056 seconds as compared to an external observer. Again,
this is measurable by atomic clocks, but not in the least bit
noticeable to the pilot or anyone else. There must be a better
way! Let's try going even faster and for much longer...
Example 3: The Voyager Project
In 1977 two remarkable spacecraft were launched by NASA,
they were called Voyager 1 and Voyager 2. During the following
decade these two small probes visited the largest planets in our
Solar System and provided spectacular and breathtaking
information about our local neighbourhood. Although expected to
function and send back data until at least the late 2020s they
have both long since left our planetary system and are heading
out into deep space where, it is tentatively hoped, they may one
day many millions of years from now be found by other
inhabitants of our galaxy.
Just in case they're found "gramophone" records have been
attached to each spacecraft. These records contain information
about us. Each contains greetings in many languages, such as
English, Hindi and even Latin. They can also play music from
many cultures, including everything from Bach to Australian
Aborigine songs. A map has also been supplied. It tells anyone
that finds it where we are and "when" we are. We have been
beaming signals into space since at least the invention of
television, but this is our first intentional solid message. If there
really is someone out there we might just be able to say hello.

The Voyager Golden Record -- A greeting from Planet Earth
One of the most notable things about the two Voyager
spacecraft is their speed. Voyager 1 is travelling at around
35,500 mph (57,500 km/h) and this is the craft we will
concentrate on. The Earth is about 24,000 miles in
circumference and so it would take much less than an hour for
Voyager 1 to circumnavigate the whole planet. The fastest
speed that a human being has so far travelled is during the
journey to the Moon and back. To get to the Moon took about
three days. For Voyager 1 it would take only seven hours.
Apart from the Sun, the nearest star to us is Alpha Proxima. This
faint star is about 4.37 light years away from us. That is,
travelling at 186,300 miles per second it would take 4.37 years
to get there (as measured by Earth clocks!). At the speed
Voyager 1 is travelling it would reach our nearest stellar
neighbour in about 80,000 years. What would be the time
dilation experienced? In other words, travelling at the speed it is
how much younger will Voyager 1 be than an Earth-bound
observer 80,000 years from now?
In this case we will use the actual speed as opposed to the
percentage of the speed of light that we have used before. This
makes no difference to the calculations as long as we make
sure that the units are the same, i.e. either both as an absolute
speed or both as a percentage. As always, we have to convert
the units to something we can easily work with:
Voyager 1 = 35,000 mph
= 57,000 km/h
= 16,000 metres per second
(about 10 miles a second)
We know the (stationary) time is 80,000 years so now we have
all the information we need to solve the time dilation equation:
dilated time = initial time x (1 – V^2/c^2)^(1/2)
= 80000 years x [1 – (16000 ms^-1)^2 / (3 x 10^8 ms^-1)^2]^(1/2)
= 80000 years x (0.9999999971556)^1/2
= 80000 years x 0.9999999985778
= 79999.99988622 years
We now subtract the measured time according to an external
observer:
80000 years – 79999.99988622 years = 0.00011378 years
If we convert this to a more convenient time scale we find that it
is just under one hour. After 80,000 years travelling through
space at 35,500 mph Voyager 1 will be only about one hour
"younger" than the Earth! In comparison to the speed of light
Voyager 1, for all its outstanding contributions to the
understanding of our Solar System, is very, very slow. So slow
in fact that it's possible that our distant descendants could
intercept the craft before any alien civilisation gets the chance.
In fact, Voyager 1 could turn out to be biggest find in the
archaeology of the distant future. Personally, I hope it's left to
go on its way.

Voyager -- Earth’s messenger

Advertisement
At the speeds we travel at in everyday life time dilation is so
small that it's not detectable to all but atomic clocks. Even if you
were to spend your whole life travelling in a fast modern jet your
time dilation as measured by a stationary observer would still
not even register on a digital watch, as we will see later in this
page.
While the equation dealing with time dilation isn't especially
difficult, it's perhaps more instructive to see some of the results
listed as a table such as in the one below. Here we see the
percentage of the speed of light (c) against its dilated
percentage, so that, for example, travelling at 90% of the speed
of light time results in time slowing down to 43.6% of its usual
rate:

Quick and easy summaries of relativity and related subjects
[ Special Relativity ] [ General Relativity ] [ Einstein ]
[ Time Dilation ] [ Black Holes ] [ Twin Paradox ]










