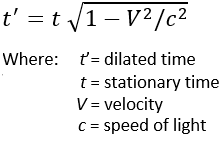Time and Moving Clocks



Advertisement



Time never seems to do what we want it to. There never seems to be enough of it when we're late for work or school, but
far too much of it when we have to stand in the pouring rain waiting for a bus. These annoyances apart, it seems that
time flows along smoothly; never bending, never changing its rate: always "on time". This steady flow is so reliable that
we fit our lives around it. We start the day when the clock tells us to, work when it tells us to, eat when it tells us to, and
go to bed when it tells us to. Time, it seems, is constant.

A sundial. Constant time?
That the flow of time is constant is seemingly obvious and this has been the prevailing view for almost all of human
history. Sir Isaac Newton, when he wasn't dodging falling apples, certainly thought time was constant. He gave us the
idea of a "clockwork universe", in which it would be possible to know not only all of the past but all of the future if only we
could say where every particle was, in what direction each particle was moving and at what speed. This model assumed,
not unreasonably, that time flows at an ever constant rate. As brilliant as Newton was, he was, much to everyone's
surprise, wrong.


Sir Isaac Newton (1642 - 1727)
Albert Einstein (1879 - 1955)
In 1905 Albert Einstein published his Special Theory of Relativity. This work considered time not as a single constantly
flowing entity, but as part of a much more complex system, linked with that of space itself. This is called space-time.
Because space and time are part of the same entity it's impossible to move in space without moving in time. Time, for
anything moving, changes.
One of the most startling consequences of special relativity is that any moving clock slows down relative to a stationary
observer. There are of course many different types of clock, such as digital watches, clockwork clocks, atomic clocks
and even our own biological clocks but they are all equally affected by the same principle, namely: moving clocks run
slow:

Moving clocks run slow.
This, above all else, is the key to understanding Special Relativity.
How slow do clocks run?
A reasonable question at this point is: if moving clocks run slowly, why don't we notice? The are two reasons for this:


We are going far too slowly for any noticeable change to take place.
Even if we go at high enough speeds to bring about a large slowing down of local time
we wouldn't notice because our own body clocks would also be running just as slowly.
The speed of light is very close to 300,000 km per second (186,300 miles per second). It isn't until we get to speeds that
are a large fraction of the speed of light that any change in the flow of time becomes apparent. However, at speeds very
close to that of light the effect grows in magnitude very rapidly indeed until time almost comes to a standstill.
This slowing down of clocks due to high speeds is called time dilation and has a precise mathematical relationship. For
the sake of completeness I have included the relevant equation below but you can skip over it and move on to the graph
below it if you prefer. The equation for time dilation is:
Time Dilation Equation
When the equation is plotted as a graph we can easily see the dramatic effect of time dilation as the speed of light is
approached:
We can see from the graph that at “low” speeds there is only a small change in time dilation (i.e. the flow of time doesn't
change very much), but at speeds over about 75% of the speed of light the effect of time dilation is quite dramatic. Even
at the "low speed" of 10% of the speed of light our clocks would slow down by only around 1%, but if we travel at 95% of
the speed of light time will slow down to about one-third of that measured by a stationary observer. Note that at zero
percent of the speed of light there is no time dilation at all. Also, while we can get as close to the speed of light as our
technology allows, it's impossible to actually reach a speed of 100% of the speed of light.
So, when we move, at whatever speed, time slows down relative to a stationary observer. But note that, for example, the
occupants of a rocket travelling at very high speeds would still experience time passing normally. However, if they could
see out to an Earth-bound clock it would appear, to them, to be running too quickly. If an Earth-bound observer could see
a clock inside the rocket it would appear to be running too slowly. This is why the theory is called "relativity", it is because
time is relative to whoever is observing it at a particular speed.
The univeral speed limit
One question often asked about relativity is "what would happen if we went faster than light?". It's sometimes said that
time would run backwards. Special relativity tells us that this is simply not possible. The universe has a speed limit of
just under the speed of light, and it has a clever way of stopping us from breaking it. As we go faster our apparent mass
(i.e. as measured by an external observer) increases in proportion to our speed. In fact our mass seems to increase at
the same rate as time slows down (in a similar way to the graph seen earlier). We know from everyday experience that
the heavier (i.e. more massive) an object is the more energy is needed to move it.
If we try to move an object at 0% of the speed of light we will find that it has the mass we expect it to have. However, the
mass of the object will appear to increase in ever increasing proportion to our speed. For example, at 99.5% of the
speed of light the object will "weigh" around 10 times what it did when it was stationary:
As our speed gets ever higher so the apparent mass increases, and so does the energy required to move it. At the speed
of light it would take infinite energy to move any mass. Since it's clearly impossible to obtain infinite energy we can never
quite reach the speed of light (but we can get as close as our energy supply, and technology, will allow). Note that the
occupants of any rocket travelling at very high speeds will not be aware of any increase in mass, just as they wouldn't be
aware in any change in the rate that time passes. It's only when they measure the mass of stationary observers that they
will see that there has been a change in mass -- the astronauts will perceive that everything around them and their rocket
has changed its mass while their own seems to have remained constant.
There is, however, something that can travel at the speed of light, and that is, of course, light! See later in this page for an
explanation.
What are the consequences of time dilation?
One of the strangest consequences of time dilation is the so-called twin paradox. In this "paradox" one identical twin is
sent at very high speed out into space. Because he or she is travelling at a very high speed all the clocks on board the
rocket, including the body clock of the twin, slow down in accordance with the principle that "moving clocks run slow".
When the twin returns he or she will have aged only a little compared to the Earth-bound twin (whose clock has been
running "normally"). A more detailed example of this can be found on the page Special Relativity in 15 Minutes!
As an illustration of time dilation we can look to a group of people whose job it is to spend their time smashing very small
particles together to see what happens. These people are called particle (or high energy) physicists. For these scientists
relativity is a routine part of their job, and indeed would be difficult if not impossible without it. The particles they smash
apart are stuck very tightly together, and so need an immense amount of energy to break them. One way to give the
particles sufficient energy is to move them very quickly in large magnetic rings called particle accelerators. This research
is considered so important that all of the major countries of the world have access to such machines. Here is the
accelerator used by the European Laboratory for Particle Physics (CERN), based at Geneva:
As you can see, it needs a very big machine to break apart a very small particle!
Many of the experiments would be over much more quickly if it wasn't for the fact that, because of the very high speeds
involved and Special Relativity, the internal "clocks" of the particles are greatly slowed down. For example, when two
particles, such as atoms, are smashed into each other at very high speeds they sometimes momentarily stick together to
form a new particle. Most of these heavier particles promptly fall apart with very short time frames, sometimes within only
a trillionth of a second. By speeding the process up not only is it possible to impart enough energy to the original particles
to actually combine them, but the resulting, heavier, particle "lives" longer, in exact accordance with how special relativity
says it should at the speed it's moving.
A further consequence of movement, any movement, is that distances shrink in the direction of motion, although this only
really becomes apparent at high percentages of the speed of light. For example, let’s say we set off for a star 100 light
years from Earth and our speed is 99% of the speed of light. Common sense tells us that we will reach the star in just
over 100 years, but this doesn’t take dilation into account. Instead, because the distance has been dilated we will reach
the star in only 14.1 years. As we go ever faster the dilation becomes ever more dramatic, so that at 99.9% of the speed
of light we would reach it in just 4.5 years and at 99.99% around 1.4 years.
You can experiment using different percentages and distances by entering them into the Dilation Calculator here.
The speed of light
To state the seemingly obvious: light travels at the speed of light. So the question is how can it do this, and why doesn't
it need infinite energy to go that fast? The answer is that particles of light (called photons) don’t have any mass. More
accurately, they have no "rest mass". Photons are constantly moving but if we could stop one and weigh it we would
find that it has no mass whatsoever. The reasons for this are beyond the scope of these pages, but every experiment
ever carried out to find any "rest-mass" in light has failed. Not only that but all of the experiments indicated have that
light is indeed massless.
However, light doesn't always travel at the "speed of light", and it doesn't take much to slow it down. You are able to
read this now only because light, either emitted from your screen or reflected off a paper copy, is striking the back of
your eyes and stimulating special cells which in turn send a "picture" to your brain. Just the air between your eyes and
these words is slowing down the light between them by about 50 km/h (30 mph). This is a very tiny percentage of the
"usual" speed of light, but we have to be careful when we say that light travels at the speed of light.
In fact, light can only travel "at the speed of light" in a vacuum, such as in space. When it does so it travels at very close
to 300,000 km per second (186,300 miles per second). At that speed it can travel around the world seven times every
second. This is undoubtedly very fast indeed, but in terms of the size of the universe it is still, perhaps surprisingly, very
slow. For example, it still takes light around 1.5 seconds to reach us from the moon, 8.5 minutes to reach us from the
Sun, 4.25 years to reach us from the nearest star (apart from the Sun), and over 13 billion years to reach us from the
furthest objects yet seen.
A million or a billion years is a very long time, of course, but perhaps we're forgetting something. We are measuring
time with our own, Earth-bound clocks! Relative to most objects in space our clocks can be considered to be very near
stationary. So how does a photon travelling at the speed of light experience time?
If you look into a clear night sky at the right time of year (winter in the northern hemisphere) you will see a pattern of
stars that looks like this, called the constellation of Andromeda:
The object shown as M31 is called, for obvious reasons, the Andromeda galaxy, and is rather like our Milky Way. On a
clear night you can see it as a faint chalk-like smudge in the sky, and for most people it's the furthest object it's possible
to see with the naked eye. Pictures taken with powerful telescopes show it to be composed of millions and millions of
stars, many of which are just like our own Sun. The Andromeda galaxy is so far away that it takes the light from it, as
measured with our Earth-bound clocks, over two million years to reach us.
However, a photon emitted from a star in Andromeda and heading out towards the Earth travels in a vacuum and,
because it's a photon, travels at the speed of light. Because the photon is moving at the speed of light it has a 100%
time dilation factor. To the photon time does not exist until it strikes the upper atmosphere of our planet and even then
is only slowed down by a tiny fraction. According to a photon in free space, time, or for that matter distance, has no
meaning whatsoever, and it gets from wherever it is to wherever it is going instantly! Personally, I'm happy to admit that
I find that mind-boggling...

The Andromeda Galaxy. (The individual stars are in our own Milky Way Galaxy).


Finally in this section, visit the Time Dilation Calculator page to
see how long it would take to reach the stars at any particular
percentage of the speed of light. It’s free, has examples to try,
is easy to use and carries out the calculations instantly. Click
the box to go to the page and start experimenting:
The Time Dilation Calculator
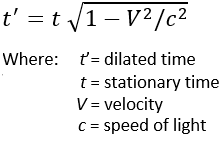
NEW! Quick and easy summaries of relativity and related subjects NEW!
[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ]
[ Black Holes ] [ Twin Paradox ]
Advertisement
advertisement
Time dilation







Time and Moving Clocks
Time never seems to do what we want it to. There never seems
to be enough of it when we're late for work or school, but far too
much of it when we have to stand in the pouring rain waiting for
a bus. These annoyances apart, it seems that time flows along
smoothly; never bending, never changing its rate: always "on
time". This steady flow is so reliable that we fit our lives around
it. We start the day when the clock tells us to, work when it tells
us to, eat when it tells us to, and go to bed when it tells us to.
Time, it seems, is constant.

A sundial. Constant time?
That the flow of time is constant is seemingly obvious and this
has been the prevailing view for almost all of human history. Sir
Isaac Newton, when he wasn't dodging falling apples, certainly
thought time was constant. He gave us the idea of a "clockwork
universe", in which it would be possible to know not only all of
the past but all of the future if only we could say where every
particle was, in what direction each particle was moving and at
what speed. This model assumed, not unreasonably, that time
flows at an ever constant rate. As brilliant as Newton was, he
was, much to everyone's surprise, wrong.


Sir Isaac Newton (1642 - 1727)
Albert Einstein (1879 - 1955)
In 1905 Albert Einstein published his Special Theory of
Relativity. This work considered time not as a single constantly
flowing entity, but as part of a much more complex system,
linked with that of space itself. This is called space-time.
Because space and time are part of the same entity it's
impossible to move in space without moving in time. Time, for
anything moving, changes.
One of the most startling consequences of special relativity is
that any moving clock slows down relative to a stationary
observer. There are of course many different types of clock,
such as digital watches, clockwork clocks, atomic clocks and
even our own biological clocks but they are all equally affected
by the same principle, namely: moving clocks run slow:


Moving clocks run slow.
This, above all else, is the key to understanding Special Relativity.
How slow do clocks run?
A reasonable question at this point is: if moving clocks run
slowly, why don't we notice? The are two reasons for this:
We are going far too slowly for any noticeable change to
take place.
Even if we go at high enough speeds to bring about a
large slowing down of local time we wouldn't notice
because our own body clocks would also be running just
as slowly.


The speed of light is very close to 300,000 km per second
(186,300 miles per second). It isn't until we get to speeds that
are a large fraction of the speed of light that any change in the
flow of time becomes apparent. However, at speeds very close
to that of light the effect grows in magnitude very rapidly indeed
until time almost comes to a standstill.
This slowing down of clocks due to high speeds is called time
dilation and has a precise mathematical relationship. For the
sake of completeness I have included the relevant equation
below but you can skip over it and move on to the graph below it
if you prefer. The equation for time dilation is:
When the equation is plotted as a graph we can easily see the
dramatic effect of time dilation as the speed of light is
approached:

We can see from the graph that at “low” speeds there is only a
small change in time dilation (i.e. the flow of time doesn't
change very much), but at speeds over about 75% of the speed
of light the effect of time dilation is quite dramatic. Even at the
"low speed" of 10% of the speed of light our clocks would slow
down by only around 1%, but if we travel at 95% of the speed of
light time will slow down to about one-third of that measured by
a stationary observer. Note that at zero percent of the speed of
light there is no time dilation at all. Also, while we can get as
close to the speed of light as our technology allows, it's
impossible to actually reach a speed of 100% of the speed of
light.
So, when we move, at whatever speed, time slows down
relative to a stationary observer. But note that, for example, the
occupants of a rocket travelling at very high speeds would still
experience time passing normally. However, if they could see
out to an Earth-bound clock it would appear, to them, to be
running too quickly. If an Earth-bound observer could see a
clock inside the rocket it would appear to be running too slowly.
This is why the theory is called "relativity", it is because time is
relative to whoever is observing it at a particular speed.
One question often asked about relativity is "what would happen
if we went faster than light?". It's sometimes said that time
would run backwards. Special relativity tells us that this is simply
not possible. The universe has a speed limit of just under the
speed of light, and it has a clever way of stopping us from
breaking it. As we go faster our apparent mass (i.e. as
measured by an external observer) increases in proportion to
our speed. In fact our mass seems to increase at the same rate
as time slows down (in a similar way to the graph seen earlier).
We know from everyday experience that the heavier (i.e. more
massive) an object is the more energy is needed to move it.
The univeral speed limit
If we try to move an object at 0% of the speed of light we will
find that it has the mass we expect it to have. However, the
mass of the object will appear to increase in ever increasing
proportion to our speed. For example, at 99.5% of the speed of
light the object will "weigh" around 10 times what it did when it
was stationary:
As our speed gets ever higher so the apparent mass increases,
and so does the energy required to move it. At the speed of light
it would take infinite energy to move any mass. Since it's clearly
impossible to obtain infinite energy we can never quite reach the
speed of light (but we can get as close as our energy supply,
and technology, will allow). Note that the occupants of any
rocket travelling at very high speeds will not be aware of any
increase in mass, just as they wouldn't be aware in any change
in the rate that time passes. It's only when they measure the
mass of stationary observers that they will see that there has
been a change in mass -- the astronauts will perceive that
everything around them and their rocket has changed its mass
while their own seems to have remained constant.
There is, however, something that can travel at the speed of
light, and that is, of course, light! See later in this page for an
explanation.
What are the consequences of time dilation?
One of the strangest consequences of time dilation is the so-
called twin paradox. In this "paradox" one identical twin is sent at
very high speed out into space. Because he or she is travelling
at a very high speed all the clocks on board the rocket, including
the body clock of the twin, slow down in accordance with the
principle that "moving clocks run slow". When the twin returns he
or she will have aged only a little compared to the Earth-bound
twin (whose clock has been running "normally"). A more detailed
example of this can be found on the page Special Relativity in 15
Minutes!
As an illustration of time dilation we can look to a group of
people whose job it is to spend their time smashing very small
particles together to see what happens. These people are called
particle (or high energy) physicists. For these scientists relativity
is a routine part of their job, and indeed would be difficult if not
impossible without it. The particles they smash apart are stuck
very tightly together, and so need an immense amount of energy
to break them. One way to give the particles sufficient energy is
to move them very quickly in large magnetic rings called particle
accelerators. This research is considered so important that all of
the major countries of the world have access to such machines.
Here is the accelerator used by the European Laboratory for
Particle Physics (CERN), based at Geneva:
As you can see, it needs a very big machine to break apart a
very small particle!
Many of the experiments would be over much more quickly if it
wasn't for the fact that, because of the very high speeds involved
and Special Relativity, the internal "clocks" of the particles are
greatly slowed down. For example, when two particles, such as
atoms, are smashed into each other at very high speeds they
sometimes momentarily stick together to form a new particle.
Most of these heavier particles promptly fall apart with very short
time frames, sometimes within only a trillionth of a second. By
speeding the process up not only is it possible to impart enough
energy to the original particles to actually combine them, but the
resulting, heavier, particle "lives" longer, in exact accordance
with how special relativity says it should at the speed it's moving.
A further consequence of movement, any movement, is that
distances shrink in the direction of motion, although this only
really becomes apparent at high percentages of the speed of
light. For example, let’s say we set off for a star 100 light years
from Earth and our speed is 99% of the speed of light. Common
sense tells us that we will reach the star in just over 100 years,
but this doesn’t take dilation into account. Instead, because the
distance has been dilated we will reach the star in only 14.1
years. As we go ever faster the dilation becomes ever more
dramatic, so that at 99.9% of the speed of light we would reach it
in just 4.5 years and at 99.99% around 1.4 years.
You can experiment using different percentages and distances
by entering them into the Dilation Calculator here.

The speed of light
To state the seemingly obvious: light travels at the speed of light.
So the question is how can it do this, and why doesn't it need
infinite energy to go that fast? The answer is that particles of
light (called photons) don’t have any mass. More accurately,
they have no "rest mass". Photons are constantly moving but if
we could stop one and weigh it we would find that it has no mass
whatsoever. The reasons for this are beyond the scope of these
pages, but every experiment ever carried out to find any "rest-
mass" in light has failed. Not only that but all of the experiments
have indicated that light is indeed massless.
However, light doesn't always travel at the "speed of light", and
it doesn't take much to slow it down. You are able to read this
now only because light, either emitted from your screen or
reflected off a paper copy, is striking the back of your eyes and
stimulating special cells which in turn send a "picture" to your
brain. Just the air between your eyes and these words is
slowing down the light between them by about 50 km/h (30
mph). This is a very tiny percentage of the "usual" speed of
light, but we have to be careful when we say that light travels at
the speed of light.
In fact, light can only travel "at the speed of light" in a vacuum,
such as in space. When it does so it travels at very close to
300,000 km per second (186,300 miles per second). At that
speed it can travel around the world seven times every second.
This is undoubtedly very fast indeed, but in terms of the size of
the universe it is still, perhaps surprisingly, very slow. For
example, it still takes light around 1.5 seconds to reach us from
the moon, 8.5 minutes to reach us from the Sun, 4.25 years to
reach us from the nearest star (apart from the Sun), and over 13
billion years to reach us from the furthest objects yet seen.
A million or a billion years is a very long time, of course, but
perhaps we're forgetting something. We are measuring time
with our own, Earth-bound clocks! Relative to most objects in
space our clocks can be considered to be very near stationary.
So how does a photon travelling at the speed of light experience
time?
If you look into a clear night sky at the right time of year (winter
in the northern hemisphere) you will see a pattern of stars that
looks like this, called the constellation of Andromeda:

The object shown as M31 is called, for obvious reasons, the
Andromeda galaxy, and is rather like our Milky Way. On a clear
night you can see it as a faint chalk-like smudge in the sky, and
for most people it's the furthest object it's possible to see with
the naked eye. Pictures taken with powerful telescopes show it
to be composed of millions and millions of stars, many of which
are just like our own Sun. The Andromeda galaxy is so far away
that it takes the light from it, as measured with our Earth-bound
clocks, over two million years to reach us.
However, a photon emitted from a star in Andromeda and
heading out towards the Earth travels in a vacuum and,
because it's a photon, travels at the speed of light. Because the
photon is moving at the speed of light it has a 100% time
dilation factor. To the photon time does not exist until it strikes
the upper atmosphere of our planet and even then is only
slowed down by a tiny fraction. According to a photon in free
space, time, or for that matter distance, has no meaning
whatsoever, and it gets from wherever it is to wherever it is
going instantly! Personally, I'm happy to admit that I find that
mind-boggling...
The Andromeda Galaxy. (The individual stars are in
our own Milky Way Galaxy).



Finally in this section, visit the Time
Dilation Calculator page to see how
long it would take to reach the stars
at any particular percentage of the
speed of light. It’s free, has examples
to try, is easy to use and carries out
the calculations instantly. Click the
box to go to the page and start
experimenting: