

Introduction: The "Proof" of Special Relativity
When Einstein first proposed his Special Theory of Relativity in 1905 few people understood it and even fewer believed
it. It wasn't until 1919 that the Special Theory was "proved by inference" from an experiment carried out on his General
Theory of Relativity. Physicists now routinely use relativity in experiments all over the world every day of the year.
However, many of these experiments are highly specialised and usually require a great deal of knowledge and training in
order to understand them. So what evidence is there for the general public? Probably the most spectacular "proof" is
nuclear weapons. These pages are not about the morality of such weapons (but that's not to say that the question of their
existence or use is not an important one). However, whether one "likes" nuclear weapons or not no one would deny that
they exist.
Both nuclear power and nuclear weapons are derived from one principle; that mass can be converted into energy, and
the equation that exactly predicts that conversion is E = mc
2
. So what has that to do with Special Relativity? The answer
is that E = mc
2
is derived directly from Special Relativity. If relativity is wrong, then nuclear weapons simply wouldn't
work. Any theory or point of view that opposes Special Relativity must explain where E = mc
2
comes from if not relativity.
Other models of relativity that contain E = mc
2
exist but here we are concerned with the standard model as proposed by
Einstein.
This page explains, with minimal mathematics, how E = mc
2
is derived from Special Relativity. In doing so it follows the
same theoretical arguments that Einstein used.
However, for reasons of completeness, and although advanced and difficult to follow, English translations of Einstein’s
original Special Relativity and E = mc
2
papers are available here (opens in new tab).

The Two Postulates
The whole of Special Relativity is based on just two rules, or as they are called in physics, postulates:
Postulate I: The principle of relativity:
The laws of physics are the same in all inertial frames.
Postulate II: The principle of the constancy of the speed of light:
The speed of light (in a vacuum) has the same constant value c in all inertial frames.
Jumping from these postulates to E = mc
2
requires a little work. In order to understand the following arguments it helps
to be familiar with Special Relativity, and in particular how moving at very high speeds dramatically changes the
properties of mass and time. If you aren't familiar with these ideas you can read about the basics here.

An Apparent Increase in Mass due to Speed
One of the consequences of Special Relativity is that mass appears to increase with speed. The faster an object goes,
the "heavier" it seems to get. This isn't noticeable in everyday life because the speeds we travel at are far too small for
the changes to be apparent. In fact, an object needs to be moving at an appreciable percentage of the speed of light
(186,300 miles per second, or 300,000 kilometres per second) before any apparent mass increase starts to become
noticeable in everyday terms.
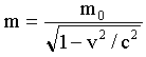
Where:
m = relativistic mass, i.e. mass at the speed it is travelling.
m
0
= "rest mass", i.e. mass of object when stationary.
v = speed of object.
c = speed of light.




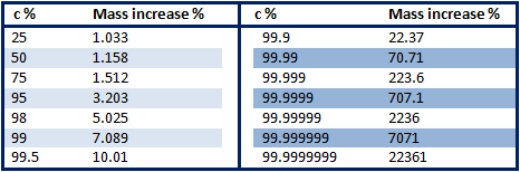
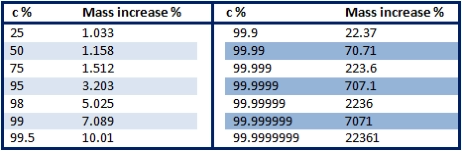
If we examine a table of representative values for the speed of light (below) we see that mass hardly increases at all
until we reach about 75% of c, but then starts to climb very rapidly.
The second set of columns show that beyond 99.9% of c the mass increase is very rapid indeed for even just a very
tiny increase in speed, tending towards (but never quite getting to) infinity:
Note that the mass can never be smaller than unity (i.e.1). This may seem a trivial point. After all, we can't just make
the mass vanish into nothing. However, while seemingly unimportant, we will return to this point later and see that it is
in fact essential to an understanding of how the equation E = mc
2
is derived.
Also note that the mass increase isn't felt by the object itself, just as the time dilation of Special Relativity isn't felt by
the object. It's only apparent to an external observer, hence it is "relative" and depends on the frame of reference
used. To an external observer it appears that the faster the object moves the more energy is needed to move it. From
this, an external, stationary observer will infer that because mass is a resistance to acceleration and the body is
resisting being accelerated, the mass of the object has increased.

Kinetic Energy
Next, we need to look at the energy involved in very high speed movement. We have seen that as an object gets
faster its mass appears to increase, and the more mass an object has the more energy is required to move it. The
standard equation for the energy of movement (kinetic energy) is:
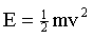
That is, kinetic energy is equal to half the mass multiplied by the velocity squared. This is often called Newtonian
kinetic energy. Note that the velocity term is squared. This means, for example, that it takes far more than twice the
energy to travel at twice any particular speed. We can see this by working through the equation for two values of v,
where: v = 50 ms
-1
and v = 100 ms
-1
respectively, both with the same mass of 10 kg:
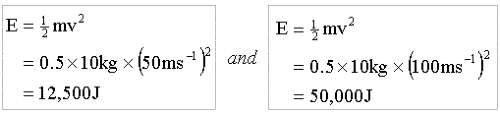
This equation is fine at "low" speeds, i.e. the speeds we encounter in everyday life. However, we know that mass
appears to increase as the speed increases and so the Newtonian equation for kinetic energy must start to become
inaccurate at speeds comparable to the speed of light. So, how do we compensate for the observed mass increase?

Advertisement
Relativistic Kinetic Energy and Mass Increase
In order to compensate for the apparent mass increase due to very high speeds we have to build it into our equations.
We know that the mass increase can be accounted for by using the equation:
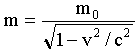
From this equation we know that mass (m) and the speed of light (c) are related in some way. What happens if we set
the speed (v) to be very low? Einstein realised that if this is done we can account for the mass increase by using the
term mc
2
(although the exact arguments and mathematics required to derive this are quite advanced and beyond the
scope of these pages). Using this term we now have an equation that takes into account both the kinetic energy and the
mass increase due to motion, at least for low speeds:
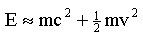
This equation seems to solve the problem. We can now predict the energy of a moving body and take into account the
mass increase. What's more, we can rearrange the equation to show that:
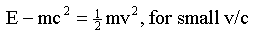
This result is fine for low speeds, but what about speeds closer to the speed of light? We know that mass increases at
high speeds, but according to the Newtonian part of the equation that isn't the case. Therefore, we need to replace the
Newtonian part of the formula in order to make the equation correct at all speeds. How can we do this?
We know that E – mc
2
is approximately equal to the Newtonian kinetic energy when v is small, so we can use E – mc
2
as the definition of relativistic kinetic energy:
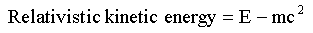
We have now removed the Newtonian part of the equation. Note that we haven’t given a formula for relativistic kinetic
energy. The reason for this will become apparent in a moment. Rearranging the result shows that:
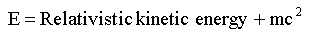
It can now be seen that relativistic energy consists of two parts. The first part is kinetic and depends on the speed of the
moving body, while the second part is due to the mass increase and does not depend on the speed of the body.
However, both parts must be a form of energy, but what form? We can simplify the equation by setting the speed (i.e.
the relativistic kinetic energy) of the moving body to be zero, thereby removing it from the equation:
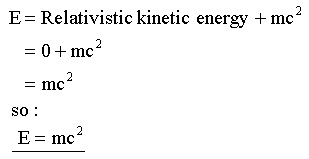
We now have the famous equation in the form it's most often seen in, but what does it mean?
We have seen that a moving body apparently increases in mass and has energy by virtue of its speed (the kinetic
energy). Looking at the problem another way we can say that as the speed of a body gets lower there will be less and
less kinetic energy until at rest the body will have no kinetic energy at all. So far so good, but what about the mass due to
the speed of the body? Again, as the body slows down the mass will become progressively smaller but it can't reach
zero. As noted near the start of the page, the lowest the mass can be is unity (1) and we can't just make the body
disappear into nothing. The lowest possible mass the body can have is its "rest mass", i.e. the mass the body has when
it is at rest. But the equation we have derived (E = mc
2
) isn't for mass, it's for energy. The energy must somehow be
locked up in the mass of the body.
Einstein therefore concluded that mass and energy are really different manifestations of the same thing, i.e. that any
mass is really tightly packed energy. At the time he saw no mechanism for releasing the energy from the mass, and was
in fact sceptical of the idea that it could ever be achieved. This didn't really matter to Einstein, however. As a theoretical
physicist he was happy that his equations were consistent and he had a model to predict what happens to a body
moving at very high speeds. Converting matter to energy has of course long since been achieved, and you can see how
much energy is released for a given amount of mass using the E = mc
2
calculator on this page.

The Full Form of the Equation
So far we have referred to the energy of very high speeds as "relativistic kinetic energy". This is fine for allowing us to
work quickly through the equations and to keep them simple, but there has to be a more formal way of expressing what
we mean. As with the term mc
2
, the detailed derivation of the full equation for E = mc
2
is quite complex. However, to
those familiar with the basic mathematics of Special Relativity the way in which we take into account the kinetic energy
of E = mc
2
will come as no surprise:
For any non-stationary body the total energy is given as:
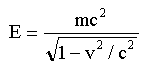
This equation takes into account the total energy (E), the mass of the body (m), and the speed of the body (v). As such it
accounts for both the relativistic mass increase and the relativistic kinetic energy.

Conclusion
The subject of this page is quite difficult to understand, even though much of the more difficult mathematical
considerations have been left to one side. The conceptual jump from the two postulates of Special Relativity to the
equivalence of mass and energy is certainly not obvious, and it's extraordinary that Einstein proposed it long before
there were any experimental results to indicate the true nature of the relationship between mass and energy.
The results of Einstein's work in this area are far more widespread than is usually thought and affect everyone on the
planet. As with all science we can use the results for "good" and "bad". The reason the words "good" and "bad" are in
quotes is because it depends on your point of view. For example, you may think that nuclear power stations (which use
E = mc
2
directly) are either a good or a bad thing. Likewise, depending on your point of view, nuclear weapons are
either a good or a bad thing; they either ended one war and prevented another, or they are immoral and bound to fall
into the wrong hands sooner or later. On the other hand, there have been great advances in using E = mc
2
in the
medical field, particularly to treat cancer. Again though, this can be seen as either a good thing (curing a disease) or a
bad thing (overburdening an already over-populated planet).
Although these issues are undoubtedly important it's not for pages such as this to hold an opinion either way, but to
merely explain some of the science behind them. It's far too late to "un-invent" E = mc
2
and the best we can do is to use
it in an informed way for the things that we believe are worthwhile.

The equation that tells us by how much mass appears to increase due to speed is:
E = mc2 derive
Advertisement
NEW! Quick and Easy SuperFast Guides NEW!
[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ]
[ Black Holes ] [ Twin Paradox ] [ Time Dilation Formula ]
NEW! Quick and Easy SuperFast Guides NEW!
[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ]
[ Black Holes ] [ Twin Paradox ] [ Time Dilation Formula ]


Advertisement
Introduction: The "Proof" of Special Relativity

The Two Postulates
The whole of special relativity is based on just two rules, or as
they are called in physics, postulates:
Postulate I: The principle of relativity:
The laws of physics are the same in all inertial frames.
Postulate II: The principle of the constancy of the speed
of light:
The speed of light (in a vacuum) has the same constant
value c in all inertial frames.
Jumping from these postulates to E = mc
2
requires a little work.
In order to understand the following arguments it helps to be
familiar with Special Relativity, and in particular how moving at
very high speeds dramatically changes the properties of mass
and time. If you aren't familiar with these ideas you can read
about the basics here.

An Apparent Increase in Mass due to Speed
One of the consequences of Special Relativity is that mass
appears to increase with speed. The faster an object goes, the
"heavier" it seems to get. This isn't noticeable in everyday life
because the speeds we travel at are far too small for the
changes to be apparent. In fact, an object needs to be moving at
an appreciable percentage of the speed of light (186,000 miles
per second, or 300,000 kilometres per second) before any
apparent mass increase starts to become noticeable in everyday
terms.
The equation that tells us by how much mass appears to
increase due to speed is:
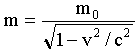
Where:




m = relativistic mass, i.e. mass at the speed it is travelling.
m
0
= "rest mass", i.e. mass of object when stationary.
v = speed of object.
c = speed of light.
Also note that the mass increase isn't felt by the object itself, just
as the time dilation of Special Relativity isn't felt by the object. It's
only apparent to an external observer, hence it is "relative" and
depends on the frame of reference used. To an external observer
it appears that the faster the object moves the more energy is
needed to move it. From this, an external, stationary observer will
infer that because mass is a resistance to acceleration and the
body is resisting being accelerated, the mass of the object has
increased.

Kinetic Energy
Next, we need to look at the energy involved in very high speed
movement. We have seen that as an object gets faster its mass
appears to increase, and the more mass an object has the more
energy is required to move it. The standard equation for the
energy of movement (kinetic energy) is:
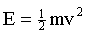
That is, kinetic energy is equal to half the mass multiplied by the
velocity squared. This is often called Newtonian kinetic energy.
Note that the velocity term is squared. This means, for example,
that it takes far more than twice the energy to travel at twice any
particular speed. We can see this by working through the
equation for two values of v, where: v = 50 ms
-1
and v = 100
ms
-1
respectively, both with the same mass of 10 kg:
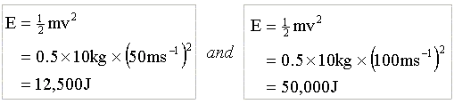
This equation is fine at "low" speeds, i.e. the speeds we
encounter in everyday life. However, we know that mass
appears to increase as the speed increases and so the
Newtonian equation for kinetic energy must start to become
inaccurate at speeds comparable to the speed of light. So, how
do we compensate for the observed mass increase?
Relativistic Kinetic Energy and Mass Increase
In order to compensate for the apparent mass increase due to
very high speeds we have to build it into our equations. We know
that the mass increase can be accounted for by using the
equation:
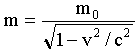
From this equation we know that mass (m) and the speed of light
(c) are related in some way. What happens if we set the speed
(v) to be very low? Einstein realised that if this is done we can
account for the mass increase by using the term mc
2
(although
the exact arguments and mathematics required to derive this are
quite advanced and beyond the scope of these pages). Using
this term we now have an equation that takes into account both
the kinetic energy and the mass increase due to motion, at least
for low speeds:
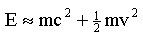
This equation seems to solve the problem. We can now predict
the energy of a moving body and take into account the mass
increase. What's more, we can rearrange the equation to show
that:
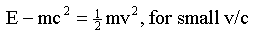
This result is fine for low speeds, but what about speeds closer to
the speed of light? We know that mass increases at high speeds,
but according to the Newtonian part of the equation that isn't the
case. Therefore, we need to replace the Newtonian part of the
formula in order to make the equation correct at all speeds. How
can we do this?
We know that E – mc
2
is approximately equal to the Newtonian
kinetic energy when v is small, so we can use E – mc
2
as the
definition of relativistic kinetic energy:
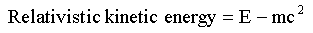
We have now removed the Newtonian part of the equation. Note
that we haven’t given a formula for relativistic kinetic energy. The
reason for this will become apparent in a moment. Rearranging
the result shows that:
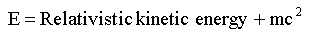
It can now be seen that relativistic energy consists of two parts.
The first part is kinetic and depends on the speed of the moving
body, while the second part is due to the mass increase and
does not depend on the speed of the body. However, both parts
must be a form of energy, but what form? We can simplify the
equation by setting the speed (i.e. the relativistic kinetic energy)
of the moving body to be zero, thereby removing it from the
equation:

We now have the famous equation in the form it's most often
seen in, but what does it mean?
Einstein therefore concluded that mass and energy are really
different manifestations of the same thing, i.e. that any mass is
really tightly packed energy. At the time he saw no mechanism
for releasing the energy from the mass, and was in fact sceptical
of the idea that it could ever be achieved. This didn't really matter
to Einstein, however. As a theoretical physicist he was happy that
his equations were consistent and he had a model to predict what
happens to a body moving at very high speeds. Converting
matter to energy has of course long since been achieved, and
you can see how much energy is released for a given amount of
mass using the E = mc
2
calculator on this page.

The Full Form of the Equation
So far we have referred to the energy of very high speeds as
"relativistic kinetic energy". This is fine for allowing us to work
quickly through the equations and to keep them simple, but there
has to be a more formal way of expressing what we mean. As
with the term mc
2
, the detailed derivation of the full equation for E
= mc
2
is quite complex. However, to those familiar with the basic
mathematics of Special Relativity the way in which we take into
account the kinetic energy of E = mc
2
will come as no surprise:
For any non-stationary body the total energy is given as:
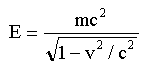
This equation takes into account the total energy (E), the mass of
the body (m), and the speed of the body (v). As such it accounts
for both the relativistic mass increase and the relativistic kinetic
energy.

Conclusion
The subject of this page is quite difficult to understand, even
though much of the more difficult mathematical considerations
have been left to one side. The conceptual jump from the two
postulates of Special Relativity to the equivalence of mass and
energy is certainly not obvious, and it's extraordinary that Einstein
proposed it long before there were any experimental results to
indicate the true nature of the relationship between mass and
energy.
The results of Einstein's work in this area are far more
widespread than is usually thought and affect everyone on the
planet. As with all science we can use the results for "good" and
"bad". The reason the words "good" and "bad" are in quotes is
because it all depends on your point of view. For example, you
may think that nuclear power stations (which use E = mc
2
directly)
are either a good or a bad thing. Likewise, depending on your
point of view, nuclear weapons are either a good or a bad thing;
they either ended one war and prevented another, or they are
immoral and bound to fall into the wrong hands sooner or later.
On the other hand, there have been great advances in using E =
mc
2
in the medical field, particularly to treat cancer. Again though,
this can be seen as either a good thing (curing a disease) or a
bad thing (overburdening an already over-populated planet).
Although these issues are undoubtedly important it's not for
pages such as this to hold an opinion either way, but to merely
explain some of the science behind them. It's far too late to "un-
invent" E = mc
2
and the best we can do is to use it in an informed
way for the things that we believe are worthwhile.
If we examine a table of representative values for the speed of
light (below) we see that mass hardly increases at all until we
reach about 75% of c, but then starts to climb very rapidly.
The
second
set
of
columns
show
that
beyond
99.9%
of
c
the
mass
increase
is
very
rapid
indeed
for
even
just
a
very
tiny
increase
in
speed,
tending
towards
(but
never
quite
getting
to)
infinity:
Note that the mass can never be smaller than unity (i.e.1). This
may seem a trivial point. After all, we can't just make the mass
vanish into nothing. However, while seemingly unimportant, we
will return to this point later and see that it is in fact essential to
an understanding of how the equation E = mc
2
is derived.
We have seen that a moving body apparently increases in mass
and has energy by virtue of its speed (the kinetic energy).
Looking at the problem another way we can say that as the
speed of a body gets lower there will be less and less kinetic
energy until at rest the body will have no kinetic energy at all. So
far so good, but what about the mass due to the speed of the
body? Again, as the body slows down the mass will become
progressively smaller but it can't reach zero. As noted near the
start of the page, the lowest the mass can be is unity (1) and we
can't just make the body disappear into nothing. The lowest
possible mass the body can have is its "rest mass", i.e. the mass
the body has when it is at rest. But the equation we have derived
(E = mc
2
) isn't for mass, it's for energy. The energy must
somehow be locked up in the mass of the body.

When Einstein first proposed his Special Theory of Relativity in
1905 few people understood it and even fewer believed it. It
wasn't until 1919 that the Special Theory was "proved by
inference" from an experiment carried out on his General Theory
of Relativity. Physicists now routinely use relativity in
experiments all over the world every day of the year. However,
many of these experiments are highly specialised and usually
require a great deal of knowledge and training in order to
understand them. So what evidence is there for the general
public? Probably the most spectacular "proof" is nuclear
weapons. These pages are not about the morality of such
weapons (but that's not to say that the question of their existence
or use is not an important one). However, whether one "likes"
nuclear weapons or not no one would deny that they exist.
Both nuclear power and nuclear weapons are derived from one
principle; that mass can be converted into energy, and the
equation that exactly predicts that conversion is E = mc
2
. So
what has that to do with Special Relativity? The answer is that E
= mc
2
is derived directly from Special Relativity. If relativity is
wrong, then nuclear weapons simply wouldn't work. Any theory
or point of view that opposes Special Relativity must explain
where E = mc
2
comes from if not relativity. Other models of
relativity that contain E = mc
2
exist but here we are concerned
with the standard model as proposed by Einstein.
This page explains, with minimal mathematics, how E = mc
2
is
derived from Special Relativity. In doing so it follows the same
theoretical arguments that Einstein used.
However, for reasons of completeness, and although advanced
and difficult to follow, English translations of Einstein’s original
Special Relativity and E = mc
2
papers are available here (opens
in new tab).


NEW! Quick and Easy SuperFast Guides NEW!
[ Time Dilation Formula ] [ General Relativity ] [ Einstein ]
[ Time Dilation ] [ Black Holes ] [ Twin Paradox ]









