

Introduction


One of the most extraordinary things about Einstein’s energy-mass equivalence equation is its simplicity. However, we
still need to make sure we are using the correct units when solving the equation, and that we understand the answer.
The purpose of this page is to solve the equation as it is and give some idea of the huge amount of energy locked up
in even the smallest amount of mass.
The Components of the Equation
If we break the equation E = mc
2
into its components and write out the terms fully we get:
E = energy (measured in joules)
m = mass (measured in kilograms)
c = the speed of light (186,300 miles per second, or 3 x 10
8
ms
-1
)



We will now examine each of the terms in a little more detail.
Energy is measured in joules (J). How much energy is one joule? Not very much really. If you pick up a large apple
and raise it above your head you will have used around one joule of energy in the process. On the other hand, we use
up huge amounts of energy every time we switch on a light. A 100 watt light bulb uses 100 joules of energy every
second, i.e. one watt is one joule per second.
The speed of light is very close to 186,300 miles per second (300,000 km per second). In order to make the equation
"work" we need to convert these numbers into units that are more suited to our purposes. In physics speeds are
measured in metres per second. This is usually abbreviated to ms
-1
; that is: "metres times seconds to the minus one".
Don’t worry if you don’t understand this notation. We could equally write m/s but using ms
-1
makes the mathematics
easier in the long run. Likewise, we could either say that the speed of light is 300,000,000 metres per second, or, as is
more usual, express the same figure in scientific notation: 3 x 10
8
ms
-1
.
Energy
Mass
The speed of light
Mass is a measure of a body’s resistance to acceleration. The greater the mass the greater the resistance to
acceleration, as anyone who has ever tried to push a heavy object knows. However, for our purposes we can also
think of mass as the amount of matter in an object. Mass is measured in kilograms (kg), with 1 kg about the same as
2.2 pounds. Note that we haven’t said what the mass is composed of. In fact, it could be anything. It doesn’t matter if
we use iron, plastic, wood, rock or gravy. The equation tells us that whatever the mass is it can be turned into energy
(whether it's practical to actually do so is another matter and is dealt with in other pages in this series).
Solving the Basic Equation
Now that we have everything in order let’s have a go at solving the equation. We will use a mass of 1 kg to keep
things simple and I will show all of the workings of the equation. So, with 1 kg of mass (around 2.2 pounds) we get:
Note how the units were dealt with and that kg m
2
s
-2
is the same as joules (although a rigorous proof of this is outside
the scope of these pages).
So from 1 kg of matter, any matter, we get 9 x 10
16
joules of energy. Writing that out fully we get:
90,000,000,000,000,000 joules
That is a lot of energy! For example, if we converted 1 kg of mass into energy and used it all to power a 100 watt light
bulb how long could we keep it lit for? In order to answer the question the first thing to do is divide the result by watts
(remember that 1 watt is 1 joule per second):
9 x 10
16
J / 100 W = 9 x 10
14
seconds
That's a lot of seconds, but how long is that in years? A year (365.25 days) is 31,557,600 seconds, so:
9 x 10
14
seconds / 31,557,600 seconds = 28,519,279 years
That is a very long time!
Of course, converting mass into energy is not quite that simple, and apart from with some tiny particles in
experimental situations has never been carried out with 100% efficiency. Perhaps that’s just as well.

Conclusion
We have seen that the E = mc
2
equation is easy to solve as it is and that for even a small amount of mass a huge
amount of energy can, at least in theory, be released. Other pages in this series show how the energy can be
released in practical ways, as well as how the equation was derived, and here is an E = mc
2
calculator.
E = mc
2
– A huge amount of energy from a small amount of mass
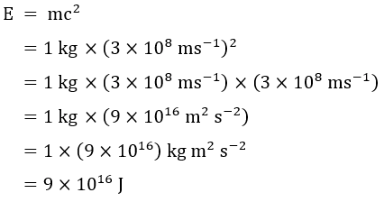
Advertisement
E = mc2 Equation
NEW! Quick and Easy SuperFast Guides NEW!
[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ]
[ Black Holes ] [ Twin Paradox ] [ Time Dilation Formula ]

Introduction


One of the most extraordinary things about Einstein’s energy-
mass equivalence equation is its simplicity. However, we still
need to make sure we are using the correct units when solving
the equation, and that we understand the answer. The purpose
of this page is to solve the equation as it is and give some idea
of the huge amount of energy locked up in even the smallest
amount of mass.
The Components of the Equation
If we break the equation E = mc
2
into its components and write
out the terms fully we get:
E = energy (measured in joules)
m = mass (measured in kilograms)
c = the speed of light (186,000 miles per second,
or 3 x 10
8
ms
-1
)
We will now examine each of the terms in a little more detail.
Energy is measured in joules (J). How much energy is one
joule? Not very much really. If you pick up a large apple and
raise it above your head you will have used around one joule of
energy in the process. On the other hand, we use up huge
amounts of energy every time we switch on a light. A 100 watt
light bulb uses 100 joules of energy every second, i.e. one watt
is one joule per second.
Energy



Mass
The speed of light
Mass is a measure of a body’s resistance to acceleration. The
greater the mass the greater the resistance to acceleration, as
anyone who has ever tried to push a heavy object knows.
However, for our purposes we can also think of mass as the
amount of matter in an object. Mass is measured in kilograms
(kg), with 1 kg about the same as 2.2 pounds. Note that we
haven’t said what the mass is composed of. In fact, it could be
anything. It doesn’t matter if we use iron, plastic, wood, rock or
gravy. The equation tells us that whatever the mass is it can be
turned into energy (whether it's practical to actually do so is
another matter and is dealt with in other pages in this series).
The speed of light is very close to 186,300 miles per second
(300,000 km per second). In order to make the equation "work"
we need to convert these numbers into units that are more
suited to our purposes. In physics speeds are measured in
metres per second. This is usually abbreviated to ms
-1
; that is:
"metres times seconds to the minus one". Don’t worry if you
don’t understand this notation. We could equally write m/s but
using ms
-1
makes the mathematics easier in the long run.
Likewise, we could either say that the speed of light is
300,000,000 metres per second, or, as is more usual, express
the same figure in scientific notation: 3 x 10
8
ms
-1
.
Advertisement
Now that we have everything in order let’s have a go at solving
the equation. We will use a mass of 1 kg to keep things simple
and I will show all of the workings of the equation. So, with 1 kg
of mass (around 2.2 pounds) we get:
Solving the Basic Equation
Note how the units were dealt with and that kg m
2
s
-2
is the
same as joules (although a rigorous proof of this is outside the
scope of these pages).
So from 1 kg of matter, any matter, we get 9 x 10
16
joules of
energy. Writing that out fully we get:
90,000,000,000,000,000 joules
That is a lot of energy! For example, if we converted 1 kg of
mass into energy and used it all to power a 100 watt light bulb
how long could we keep it lit for? In order to answer the
question the first thing to do is divide the result by watts
(remember that 1 watt is 1 joule per second):
9 x 10
16
J / 100 W = 9 x 10
14
seconds
That's a lot of seconds, but how long is that in years? A year
(365.25 days) is 31,557,600 seconds, so:
9 x 10
14
seconds / 31,557,600 seconds = 28,519,279 years
That is a very long time!
Of course, converting mass into energy is not quite that simple,
and apart from with some tiny particles in experimental
situations has never been carried out with 100% efficiency.
Perhaps that’s just as well.

Conclusion
We have seen that the E = mc
2
equation is easy to solve as it
is and that for even a small amount of mass a huge amount of
energy can, at least in theory, be released. Other pages in
this series show how the energy can be released in practical
ways, as well as how the equation was derived, and here is
an E = mc
2
calculator
E = mc
2
– A lot of energy from a small mass
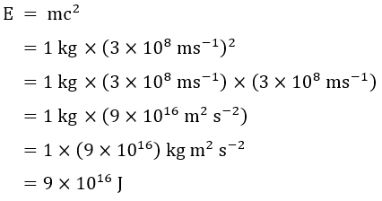


NEW! Quick and Easy SuperFast Guides NEW!
[ Time Dilation Formula ] [ General Relativity ] [ Einstein ]
[ Time Dilation ] [ Black Holes ] [ Twin Paradox ]









