
Without doubt E = mc
2
is the world’s most famous equation. This page explains what E = mc
2
means in simple terms
and some of its consequences. The equation is derived directly from Einstein’s Special Theory of Relativity, and other
pages in this series deal with the mathematical and logical derivation. Here though, we will examine the equation as it
stands and keep the mathematics to a minimum.
Energy = mass x the speed of light squared
In other words:
E = energy (measured in joules, J)
m = mass (measured in kilograms, kg)
c = the speed of light (measured in meters per second, ms
-1
), but this needs to be "squared".
Note that the case of each letter is important and it would be incorrect to show the equation as, for example, e = MC².
This is because physicists use the case of letters as well as the letters themselves to denote particular physical
entities, quantities and constants in equations.
In order for the equation to be correct we need to "square" the term c (the speed of light), i.e. we multiply the speed of
light by itself; hence c
2
is the same as c times c. This allows us to be write the equation in another, slightly unusual, but
equally correct way:
E = m x c x c
As a matter of interest, and to complete the terms used in the equation, the equals sign was only invented during the
16th century, by the Welsh mathematician Robert Recorde, apparently unhappy having to write out "is equal to" in his
work. He could have chosen any number of symbols but chose two parallel lines because, as he himself put it, "noe 2
thynges can be moare equalle".
We will now examine each unit (i.e. letter) in the equation in turn before addressing the question of what the equation
means, but if you want to see worked examples of the equations you can do so here.

Introduction
The word "energy" is actually quite new. Its modern use dates from around the middle of the nineteenth century, when
it was beginning to be realised that the power that drove many different processes could be explained by the concept
of energy being transferred from one system and form to another. For example, the trains of the day were powered by
coal. The coal was burned under a water-filled boiler to produce steam, which in turn pushed pistons attached to the
wheels of the train, the wheels turned and the train was set in motion. In this example we start with locked up ("latent")
chemical energy in the coal. The chemical energy is turned into heat energy (sometimes called "thermal energy") by
burning the coal and boiling the water. Finally, the thermal energy is turned into the energy of movement ("kinetic
energy") by forcing the steam into pistons to drive the wheels:
A moving steam train
Chemical energy - thermal energy - kinetic energy
E = Energy



There are many other forms of energy, such as electrical, gravitational, nuclear, and strain energy, such as that found
in springs. However, as different as all these types of energy seem they can all be measured in the same way and
thought of as the same thing. The unit that we use to measure energy, from whatever energy source, is the joule (J).
Two ways in which we use this unit in everyday terms are:
The total amount of energy in a system:
As noted above, one example is a lump of coal, which when burned will release a certain number of
joules (J) of energy, mostly in the forms of heat and light. Another, perhaps more common example, is
that it takes about 1 joule to raise an apple by 1 meter.
Energy used up over time:
Most electrical devices have their power consumption rated in watts (W). A watt is a rate of energy
consumption of one joule per second. So, if you have a light bulb in your room that's rated at 100 W it's
using energy at a rate of 100 joules every second.
To go back to the second example in the first bullet point, lifting an apple by 1 metre every second
would mean that there is a power output of 1 watt. For most people this would be quite easy and could
be kept up for quite a long time, but now imagine lifting 100 apples a second, i.e. 100 W. This, in
human terms, is a large power output, but nothing special for many electrical devices. It's not
uncommon, for example, for a kettle to be rated at 2000 W or more. That's a lot of apples!
So, to summarise, energy comes in many forms, and it can be transferred from one system to another. The basic unit
of measurement for energy is the joule.



m = Mass
c = the Speed of Light
Mass is strictly defined as a measure of a body’s inertia, i.e. its resistance to acceleration. Another and simpler way of
defining mass is to say that it's the total amount of matter in an object. This latter definition isn’t strictly true, but is good
enough for our purposes here. Mass is measured in kilograms (kg).
Note that mass isn’t the same as weight, although it's often thought to be. Weight is actually a measure of the
gravitational force (pull) felt by a body and is measured in newtons (N) (note that scientific units that are named after
people are almost always in lower case when spelled out fully, hence newtons and not Newtons, watts and not Watts
etc.). For example, astronauts walking on the surface of the Moon have the same mass as on Earth but only weigh
one sixth of what they would do back home. The reason for this is that while the mass of the astronauts hasn’t
changed, the pull of the Moon’s gravity is only one sixth of what the Earth’s gravitational pull is.
As with energy, the idea that mass is common to all objects is relatively new and again dates back to around the
nineteenth century. Before that time different solids, liquids and gases were all thought to be only loosely connected in
conceptual terms. As with energy, we now consider that mass is neither created or destroyed, but is merely changed
from one form to another, e.g. we can turn water from a solid (ice) into a liquid (water) and into a gas (steam), but its
total mass doesn’t change.

We use the letter c to represent the speed of light. The ‘c’ comes from the Latin word “celeritas”, meaning swift, and it’s
a very apt definition - there is nothing faster than light. In a vacuum, such as space, it travels at close to 186,300 miles
per second (300,000 km per second). That’s about seven times around the Earth every second.
The speed of light was first accurately estimated by the Danish astronomer Ole Roemer (sometimes written as Rømer)
during the 1670s. Up until that time everyone assumed that the speed of light was infinite, i.e. that light arrived at its
destination instantly. This isn’t such an unreasonable assumption given that when we look around us light does indeed
appear to reach us instantly.
However, during the seventeenth century it was discovered that there was a problem in calculating the orbital time of
Io, the innermost moon of Jupiter. It sometimes took "too long" to make an orbit of the planet and at other times was
"too quick". It was thought that the problem must be due to a wobble in the orbit of Io, but Roemer took a different, and
very radical, view of the matter. He argued that light, instead of being everywhere instantly, had a finite speed and that
this would explain the problem of Io. The Earth was known to travel around the Sun and this meant that sometimes the
Earth was closer to Jupiter and sometimes further away. Roemer realised that when the Earth was on the opposite
side of the Sun from Jupiter the light from Io would take longer to reach us than when the two bodies were on the same
side:
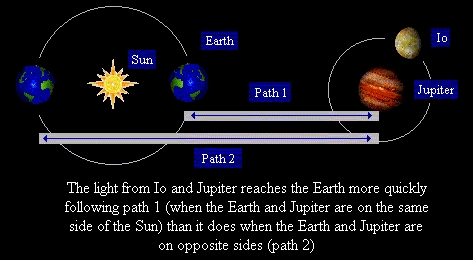
This means that the light has to travel further and therefore takes longer, providing, of course, that light has a speed in
the first place. During a meeting of the new Academy of Science in Paris in 1676 Roemer demonstrated that the
amassed observational data of the astronomer Cassini indicated that Io would next appear at 5.25pm on 9th
November of that year. He himself predicted that it wouldn’t appear until 10 minutes and 45 second later, using his
theory that light had a finite speed. The day came and virtually every major observatory in Europe was ready to test the
prediction. At 5.25pm, the time predicted by Cassini, Io wasn’t visible. Even at 5.35pm Io wasn’t visible. But at exactly
5.35pm and 45 seconds it appeared, just as Roemer said it would. From this it was possible to make the first accurate
measurement of the speed of light and the calculated figure was within one percent of what we know it to be today.
You may think that that was the end of the matter and that Roemer was celebrated as a scientific genius, showered
with honours and given a secure future. Sadly, that’s far from what happened. He was only 21 when he made his
discovery, while Cassini was a well-respected if egotistical elder scientist, who used his powerful friends to back him
up to rubbish Roemer’s ideas. Scientists, it seems, are human after all and this wasn’t the first, or sadly, the last time
that an ego got in the way of a new discovery. Roemer eventually gave up science completely and later became the
director of the port of Copenhagen and then head of the State Council of the Realm. It wasn’t until 50 years later that
further experiments convinced the scientific community that Roemer had been right all along.

Ole Roemer 1644 - 1710

Advertisement
What Does the Equation Mean?
The equation tells us that energy and mass are, effectively, the same thing, and it also tells us how much energy is
contained in a given mass, or vice versa. In other words, mass can be thought of as very tightly packed energy. That
energy and mass are equivalent is quite an extraordinary claim and seems to go against two laws that had been
established by scientists before Einstein came along:
The Law of the Conservation of Mass:
As we have seen, mass can be thought of as the quantity of matter in an object. The law of the
conservation of mass states that mass is always conserved. That is, whatever we do with matter in a
closed system we will always have the same amount of substance at the end. For example, if we burn
a log, the wood gets lighter as the fuel it contains is used up. However, if we gather together the
ashes, all of the tiny smoke particles and the water vapour produced by the burning process and then
weigh everything we find that the mass is exactly equal to the mass of the log that was burned. Mass
is just mass, or so it seems, and while it can be chemically altered, such as burned, the total amount
in any system remains the same.
The Law of the Conservation of Energy:
But what about the energy released in burning the log? The energy released in the burning process is
"chemical energy", i.e. the breaking and reforming of chemical bonds between atoms and molecules.
Burning the wood released the chemical energy locked up in it. No energy was created in the process
and none was destroyed; it was just changed from one sort of energy (chemical bonds) to other forms
of energy (heat and light). In other words the total amount of energy, just like the total amount of mass,
remained the same.
After many experiments, notably by the scientist for whom the unit of energy is named, James Prescott Joule (1818 -
1889), it was established that the total amount of energy in a closed system always remains the same. This is known
as the law of the conservation of energy.
What Einstein showed via his now famous equation was that mass and energy are in fact the same thing. Converting
one into the other doesn’t therefore violate either of the two conservation laws. Both quantities are conserved, although
the state of the mass/energy may have changed. Each atom of a substance can be thought of as a little ball of tightly
packed energy that can be released under certain circumstances. Likewise, we can take energy (such as particles of
light, called photons) and turn it into matter. This was first achieved in the 1930s.
That light can be turned into matter is perhaps a rather odd idea, but the picture below shows the first successful
experiment in which this was done:

Cloud chamber photon decay
The picture shows the tracks of two matter particles that have been "created" after a high energy photon decayed, i.e.
"fell apart", in a cloud chamber. The high energy photon is not in the visible range and has entered the chamber from
the bottom of the picture.
The Cloud Chamber
A cloud chamber is a sealed tank filled with a gas, usually with a magnet to one side of it. When a
particle, such as an atom, electron or proton passes through the tank it collides with some of the
particles in the gas to produce little clouds that mark its path. For an electrically neutral particle,
such as a neutron, the path will be straight. However, for any particle that is not electrically
neutral its path will be bent towards or away from the magnet that forms part of the apparatus.
The subject of turning matter into energy through both fusion and fission is dealt with in other pages in this series.


Einstein’s Explanation of his Equation

Einstein speaking about the equation E = mc
2
(211kB, .MP3 file)
From the soundtrack of the film Atomic Physics.
Copyright © J. Arthur Rank Organisation, Ltd., 1948.
The recording is old, and that, together with Einstein’s accent, sometimes makes it difficult to hear the words properly.
This is a transcript of the recording:
“It followed from the Special Theory of Relativity that mass and energy are both but different
manifestations of the same thing - a somewhat unfamiliar conception for the average mind.
Furthermore, the equation E is equal to mc
2
, in which energy is put equal to mass, multiplied with
the [by the] square of the velocity of light, showed that very small amounts of mass may be
converted into a very large amount of energy and vice versa. The mass and energy were in fact
equivalent, according to the formula mentioned before [E = mc
2
]. This was demonstrated by
Cockcroft and Walton in 1932, experimentally."

Albert Einstein (1879 - 1955)


Albert Einstein (1879 - 1955)

What do the Letters Stand For?
Each of the letters of E = mc
2
stands for a particular physical quantity. Writing them out in full we get:

Advertisement
Advertisement
E = mc2 The Basics
Advertisement


[ Special Relativity ] [ General Relativity ] [ Einstein ] [ Time Dilation ]
[ Black Holes ] [ Twin Paradox ] [ Time Dilation Formula ]
NEW! Quick and Easy SuperFast Guides NEW!
Energy = mass x the speed of light squared

Introduction
A moving steam train
Chemical energy - thermal energy - kinetic energy
E = Energy



m = Mass
c = the Speed of Light

Ole Roemer 1644 - 1710

What Does the Equation Mean?

Cloud chamber photon decay
The Cloud Chamber
A cloud chamber is a sealed tank filled with a gas,
usually with a magnet to one side of it. When a particle,
such as an atom, electron or proton passes through the
tank it collides with some of the particles in the gas to
produce little clouds that mark its path. For an
electrically neutral particle, such as a neutron, the path
will be straight. However, for any particle that is not
electrically neutral its path will be bent towards or away
from the magnet that forms part of the apparatus.
The subject of turning matter into energy through both fusion
and fission is dealt with in other pages in this series.

Einstein’s Explanation of his Equation

Albert Einstein (1879-1955)


Albert Einstein (1879-1955)

What do the Letters Stand For?
Without doubt E = mc
2
is the world’s most famous equation.
This page explains what E = mc
2
means in simple terms and
some of its consequences. The equation is derived directly from
Einstein’s Special Theory of Relativity, and other pages in this
series deal with the mathematical and logical derivation. Here
though, we will examine the equation as it stands and keep the
mathematics to a minimum.
Each of the letters of E = mc
2
stands for a particular physical
quantity. Writing them out in full we get:
In other words:
E = energy (measured in joules, J)
m = mass (measured in kilograms, kg)
c = the speed of light (measured in meters per
second, ms
-1
), but this needs to be "squared".
Note that the case of each letter is important and it would be
incorrect to show the equation as, for example, e = MC
2
. This
is because physicists use the case of letters as well as the
letters themselves to denote particular physical entities,
quantities and constants in equations.
In order for the equation to be correct we need to "square" the
term c (the speed of light), i.e. we multiply the speed of light by
itself; hence c² is the same as c times c. This allows us to be
write the equation in another, slightly unusual, but equally
correct way:
E = m x c x c
As a matter of interest, and to complete the terms used in the
equation, the equals sign was only invented during the 16th
century, by the Welsh mathematician Robert Recorde.
Apparently unhappy having to write out "is equal to" in his
work. He could have chosen any number of symbols but chose
two parallel lines because, as he himself put it, "noe 2 thynges
can be moare equalle".
We will now examine each unit (i.e. letter) in the equation in
turn before addressing the question of what the equation
means, but if you want to see worked examples of the
equations you can do so here.
The word "energy" is actually quite new. Its modern use dates
from around the middle of the nineteenth century, when it was
beginning to be realised that the power that drove many
different processes could be explained by the concept of
energy being transferred from one system and form to another.
For example, the trains of the day were powered by coal. The
coal was burned under a water-filled boiler to produce steam,
which in turn pushed pistons attached to the wheels of the
train, the wheels turned and the train was set in motion. In this
example we start with locked up ("latent") chemical energy in
the coal. The chemical energy is turned into heat energy
(sometimes called "thermal energy") by burning the coal and
boiling the water. Finally, the thermal energy is turned into the
energy of movement ("kinetic energy") by forcing the steam
into pistons to drive the wheels:
There are many other forms of energy, such as electrical,
gravitational, nuclear, and strain energy, such as that found in
springs. However, as different as all these types of energy
seem they can all be measured in the same way and thought
of as the same thing. The unit that we use to measure energy,
from whatever energy source, is the joule (J). Two ways in
which we use this unit in everyday terms are:
The total amount of energy in a system:
As noted above, one example is a lump of coal, which
when burned will release a certain number of joules (J)
of energy, mostly in the forms of heat and light.
Another, perhaps more common example, is that it
takes about 1 joule to raise an apple by 1 meter.


Energy used up over time:
Most electrical devices have their power consumption
rated in watts (W). A watt is a rate of energy
consumption of one joule per second. So, if you have a
light bulb in your room that's rated at 100 W it's using
energy at a rate of 100 joules every second.
To go back to the second example in the first bullet
point, lifting an apple by 1 metre every second would
mean that there is a power output of 1 watt. For most
people this would be quite easy and could be kept up
for quite a long time, but now imagine lifting 100 apples
a second, i.e. 100 W. This, in human terms, is a large
power output, but nothing special for many electrical
devices. It's not uncommon, for example, for a kettle to
be rated at 2000 W or more. That's a lot of apples!
So, to summarise, energy comes in many forms, and it can be
transferred from one system to another. The basic unit of
measurement for energy is the joule.
Mass is strictly defined as a measure of a body’s inertia, i.e. its
resistance to acceleration. Another and simpler way of
defining mass is to say that it's the total amount of matter in an
object. This latter definition isn’t strictly true, but is good
enough for our purposes here. Mass is measured in kilograms
(kg).
Note that mass isn’t the same as weight, although it's often
thought to be. Weight is actually a measure of the gravitational
force (pull) felt by a body and is measured in newtons (N)
(note that scientific units that are named after people are
almost always in lower case when spelled out fully, hence
newtons and not Newtons, watts and not Watts etc.). For
example, astronauts walking on the surface of the Moon have
the same mass as on Earth but only weigh one sixth of what
they would do back home. The reason for this is that while the
mass of the astronauts hasn’t changed, the pull of the Moon’s
gravity is only one sixth of what the Earth’s gravitational pull is.
As with energy, the idea that mass is common to all objects is
relatively new and again dates back to around the nineteenth
century. Before that time different solids, liquids and gases
were all thought to be only loosely connected in conceptual
terms. As with energy, we now consider that mass is neither
created or destroyed, but is merely changed from one form to
another, e.g. we can turn water from a solid (ice) into a liquid
(water) and into a gas (steam), but its total mass doesn’t
change.


We use the letter c to represent the speed of light. The ‘c’
comes from the Latin word “celeritas”, meaning swift, and it’s a
very apt definition - there is nothing faster than light. In a
vacuum, such as space, it travels at close to 186,300 miles
per second (300,000 km per second). That’s about seven
times around the Earth every second.
The speed of light was first accurately estimated by the Danish
astronomer Ole Roemer (sometimes written as Rømer) during
the 1670s. Up until that time everyone assumed that the
speed of light was infinite, i.e. that light arrived at its
destination instantly. This isn’t such an unreasonable
assumption given that when we look around us light does
indeed appear to reach us instantly.
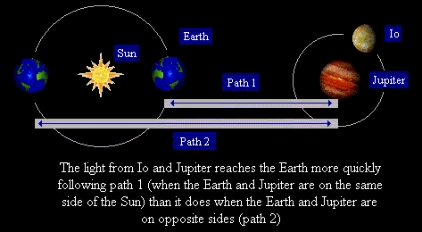
However, during the seventeenth century it was discovered
that there was a problem in calculating the orbital time of Io,
the innermost moon of Jupiter. It sometimes took "too long" to
make an orbit of the planet and at other times was "too quick".
It was thought that the problem must be due to a wobble in the
orbit of Io, but Roemer took a different, and very radical, view
of the matter. He argued that light, instead of being
everywhere instantly, had a finite speed and that this would
explain the problem of Io. The Earth was known to travel
around the Sun and this meant that sometimes the Earth was
closer to Jupiter and sometimes further away. Roemer
realised that when the Earth was on the opposite side of the
Sun from Jupiter the light from Io would take longer to reach
us than when the two bodies were on the same side:
This means that the light has to travel further and therefore
takes longer, providing, of course, that light has a speed in the
first place. During a meeting of the new Academy of Science in
Paris in 1676 Roemer demonstrated that the amassed
observational data of the astronomer Cassini indicated that Io
would next appear at 5.25pm on 9th November of that year. He
himself predicted that it wouldn’t appear until 10 minutes and
45 second later, using his theory that light had a finite speed.
The day came and virtually every major observatory in Europe
was ready to test the prediction. At 5.25pm, the time predicted
by Cassini, Io wasn’t visible. Even at 5.35pm Io wasn’t visible.
But at exactly 5.35pm and 45 seconds it appeared, just as
Roemer said it would. From this it was possible to make the
first accurate measurement of the speed of light and the
calculated figure was within one percent of what we know it to
be today.
You may think that that was the end of the matter and that
Roemer was celebrated as a scientific genius, showered with
honours and given a secure future. Sadly, that’s far from what
happened. He was only 21 when he made his discovery, while
Cassini was a well-respected if egotistical elder scientist, who
used his powerful friends to back him up to rubbish Roemer’s
ideas. Scientists, it seems, are human after all and this wasn’t
the first, or sadly, the last time that an ego got in the way of a
new discovery. Roemer eventually gave up science completely
and later became the director of the port of Copenhagen and
then head of the State Council of the Realm. It wasn’t until 50
years later that further experiments convinced the scientific
community that Roemer had been right all along.
The equation tells us that energy and mass are, effectively, the
same thing, and it also tells us how much energy is contained in
a given mass, or vice versa. In other words, mass can be
thought of as very tightly packed energy. That energy and mass
are equivalent is quite an extraordinary claim and seems to go
against two laws that had been established by scientists before
Einstein came along:
After many experiments, notably by the scientist for whom
the unit of energy is named, James Prescott Joule (1818 -
1889), it was established that the total amount of energy in
a closed system always remains the same. This is known
as the law of the conservation of energy.
What Einstein showed via his now famous equation was
that mass and energy are in fact the same thing. Converting
one into the other doesn’t therefore violate either of the two
conservation laws. Both quantities are conserved, although
the state of the mass/energy may have changed. Each
atom of a substance can be thought of as a little ball of
tightly packed energy that can be released under certain
circumstances. Likewise, we can take energy (such as
particles of light, called photons) and turn it into matter. This
was first achieved in the 1930s.
That light can be turned into matter is perhaps a rather odd
idea, but the picture below shows the first successful
experiment in which this was done:
The picture shows the tracks of two matter particles that have
been "created" after a high energy photon decayed, i.e. "fell
apart", in a cloud chamber. The high energy photon is not in the
visible range and has entered the chamber from the bottom of
the picture.

“It followed from the Special Theory of Relativity that mass and
energy are both but different manifestations of the same thing -
a somewhat unfamiliar conception for the average mind.
Furthermore, the equation E is equal to mc
2
, in which energy is
put equal to mass, multiplied with the [by the] square of the
velocity of light, showed that very small amounts of mass may
be converted into a very large amount of energy and vice versa.
The mass and energy were in fact equivalent, according to the
formula mentioned before [E = mc
2
]. This was demonstrated by
Cockcroft and Walton in 1932, experimentally."

Einstein speaking about the equation E = mc
2
(211kB, .MP3 file)
From the soundtrack of the film Atomic Physics.
Copyright © J. Arthur Rank Organisation, Ltd., 1948.

Advertisement


Advertisement


NEW! Quick and Easy SuperFast Guides NEW!
[ Time Dilation Formula ] [ General Relativity ] [ Einstein ]
[ Time Dilation ] [ Black Holes ] [ Twin Paradox ]









